题目内容
锐角三角形中，最大角α的取值范围是（ ）
A. 0°< α < 90° B. 60°< α < 180° C. 60°< α < 90° D. 60°≤α < 90°
D
【解析】试题分析：根据三角形的内角和定理，又α是最大角，得：3α≥180°，即α≥60°，故最大角α的取值范围是60°≤α＜180度．
如图，△ABC中，D，E分别是BC上两点，且BD=DE=EC，则图中面积相等的三角形有（ ）
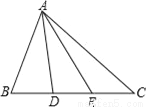
A. 4对 B. 5对 C. 6对 D. 7对
A
【解析】等底同高的三角形的面积相等，所以△ABD，△ADE，△AEC三个三角形的面积相等，有3对，又△ABE与△ACD的面积也相等，有1对，所以共有4对三角形面积相等。
故选A. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（ ）
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0．365 | 0．328 | 0．330 | 0．334 | 0．336 | 0．332 | 0．333 |
A. 一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃
B. 在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”
C. 抛一个质地均匀的正六面体骰子，向上的面点数是5
D. 抛一枚硬币，出现反面的概率
B
【解析】试题解析：A、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率为，不符合题意；
B、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”的概率是，符合题意；
C、抛一个质地均匀的正六面体骰子，向上的面点数是5的概率为，不符合题意；
D、抛一枚硬币，出现反面的概率为，不符合题意，
故选B． 如图所示，太阳光线AC与A′C′是平行的，AB表示一棵塔松，A′B′表示一棵小杨树，同一时刻两棵树的影长相等，已知塔松高6米，则小杨树高______.
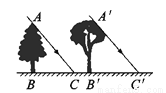
6米
【解析】试题解析：∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的，
∴∠ABC=∠A′B′C′=90°，
∵∠ABC=∠A′B′C′，∠ACB=∠A′C′B′，AC∥A′C′，
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等)，
∴AB=A′B′=6米 (全等三角形的对应边相等)，... 下列条件中，能判定△ABC为直角三角形的是( )
A. ∠A=∠B=∠C B. ∠A＋∠B=2∠C
C. ∠A∶∠B∶∠C=1∶2∶3 D. ∠A=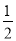
∠B=
∠C
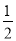C
【解析】试题解析：A. ，∠A=∠B=∠C不能确定△ABC为直角三角形，所以A选项错误；
B． ,而∠A+∠B=2∠C,则所以B选项错误；
C. ,而∠A∶∠B∶∠C=1∶2∶3,则，所以C选项正确；
D. ，而则所以D选项错误.
故选C. 如图,已知直线l是AB的垂直平分线,M是直线l上的一点,D,E是AB上不同的点,则AM=BM吗?MD=ME吗?
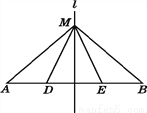
AM=BM,无法判断MD是否等于ME.
【解析】由M在线段AB的垂直平分线l上，根据“线段的垂直平分线上任意一点，到线段两端点的距离相等”即可判断AM=BM成立；根据直线l不一定是DE的垂直平分线，则无法判断MD与ME的大小关系.
【解析】
∵l是AB的垂直平分线，
∴AM=BM．
由于D、E是AB上任意两点，所以MD不一定等于ME，只有当l经过DE的中点时，MD=ME．... 已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
A. △ABC的边AB的垂直平分线 B. ∠ACB的平分线所在的直线
C. △ABC的边BC上的中线所在的直线 D. △ABC的边AC上的高所在的直线
C
【解析】根据条件可以推出AB=AC，由此即可判断．
【解析】
∵l=AB+BC+AC，
∴BC=l?2AB=AB+BC+AC?2AB，
∴AB=AC，
∴△ABC中BC边中线所在的直线是△ABC的对称轴.
故选C. 如图，在Rt△ABC中，∠ACB＝90°，D是边AB的中点，BE⊥CD，垂足为点E.已知AC＝15，cosA＝
.
(1)求线段CD的长；
(2)求sin∠DBE的值．
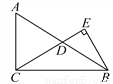
（1）CD＝；（2）sin∠DBE=.
【解析】试题分析：（1）根据直角三角形斜边上的中线等于斜边的一半，求出AB的长，即可求出CD的长；（2）由于D为AB上的中点，求出AD=BD=CD=，设DE=x，EB=y，利用勾股定理即可求出x的值，据此解答即可．
试题解析：：【解析】
（1）∵AC=15，cosA=，
∴cosA=,
∴AB=25，
∵△ACB为直角三角形，... 如果∠1与∠2互补，∠1与∠3互余，那么 ( )
A. ∠2＞∠3 B. ∠2=∠3 C. ∠2＜∠3 D. ∠2≥∠3
A
【解析】∵∠1与∠2互补，∴∠1+∠2=180°，
∵∠1与∠3互余，∴∠1+∠3=90°，
∴∠1+∠2-（∠1+∠3）=180°-90°，
∴∠2-∠3=90°，
∴∠2＞∠3．
故选A．