题目内容
如图⑴~⑿中全等的图形是_____和______;_____和______;_____和______;
_____和______;_____和______;_____和______;(填图形的序号)
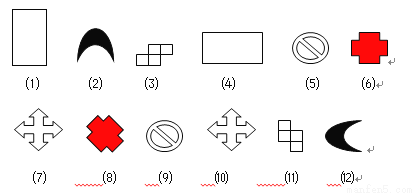
 (1)、(4);(2)、(12);(3)、(11);(5)、(9);(6)、(8);(7)、(10)
【解析】通过观察可以发现:(1)和(4)、(2)和(12)、(3)和(11)、(5)和(9)、(6)和(8)、(7)和(10)是全等形,
故答案为:(1)、(4);(2)、(12);(3)、(11);(5)、(9);(6)、(8);(7)、(10).
(1)、(4);(2)、(12);(3)、(11);(5)、(9);(6)、(8);(7)、(10)
【解析】通过观察可以发现:(1)和(4)、(2)和(12)、(3)和(11)、(5)和(9)、(6)和(8)、(7)和(10)是全等形,
故答案为:(1)、(4);(2)、(12);(3)、(11);(5)、(9);(6)、(8);(7)、(10).
从1至9这些数字中任意取一个,取出的数字是偶数的概率是( )
A. 0 B. 1 C. 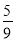 D.
D. 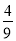
 D
【解析】在1至9这些数字中,共有2,4,6,8四个偶数,因此从这九个数字中任意取一个,取出的数字是偶数的概率是.故选D.
D
【解析】在1至9这些数字中,共有2,4,6,8四个偶数,因此从这九个数字中任意取一个,取出的数字是偶数的概率是.故选D. 如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是 △ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.
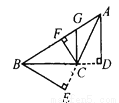
 AD CF BE BFC FGC FAC GAC
【解析】试题解析:AD是△ABC中BC边上的高,是△ABC中AB边上的高,BE是△ABC中AC边上的高,CF是△ABC的高,也是△BFC、△FGC、△FAC、△GAC的高.
故答案是:AD、CF、BE、BFC、FGC、FAC、GAC.
AD CF BE BFC FGC FAC GAC
【解析】试题解析:AD是△ABC中BC边上的高,是△ABC中AB边上的高,BE是△ABC中AC边上的高,CF是△ABC的高,也是△BFC、△FGC、△FAC、△GAC的高.
故答案是:AD、CF、BE、BFC、FGC、FAC、GAC. 如图,△ABC中,D,E分别是BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )
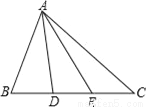
A. 4对 B. 5对 C. 6对 D. 7对
 A
【解析】等底同高的三角形的面积相等,所以△ABD,△ADE,△AEC三个三角形的面积相等,有3对,又△ABE与△ACD的面积也相等,有1对,所以共有4对三角形面积相等。
故选A.
A
【解析】等底同高的三角形的面积相等,所以△ABD,△ADE,△AEC三个三角形的面积相等,有3对,又△ABE与△ACD的面积也相等,有1对,所以共有4对三角形面积相等。
故选A. 如图,把大小为4×4的正方形方格分割成两个全等图形,例如图1,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格分割成两个全等图形.

 见解析
【解析】试题分析:可以利用图形的对称性和互补性来分隔成两个全等的图形.
试题解析:∵要求分成全等的两块,
∴每块图形要包含有8个小正方形.
见解析
【解析】试题分析:可以利用图形的对称性和互补性来分隔成两个全等的图形.
试题解析:∵要求分成全等的两块,
∴每块图形要包含有8个小正方形. 如图,△ABC≌△AED,∠C=400,∠EAC=300,∠B=300,则∠EAD=( );
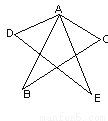
A. 300 B. 700 C. 400 D. 1100
 D
【解析】∵△ABC≌△AED,
∴∠D=∠C=40°,∠C=∠B=30°,
∴∠E AD=180°-∠D-∠E=110°,
故选D.
D
【解析】∵△ABC≌△AED,
∴∠D=∠C=40°,∠C=∠B=30°,
∴∠E AD=180°-∠D-∠E=110°,
故选D. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
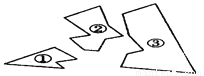
A. 带①去 B. 带②去 C. 带③去 D. 带①和②去
 C
【解析】试题解析:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误;
B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误;
C、带③去,不但保留了原三角形的两个角还保留了其中一个边,符合ASA判定,故C选项正确;
D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D...
C
【解析】试题解析:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误;
B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误;
C、带③去,不但保留了原三角形的两个角还保留了其中一个边,符合ASA判定,故C选项正确;
D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D... 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C. 抛一个质地均匀的正六面体骰子,向上的面点数是5
D. 抛一枚硬币,出现反面的概率
 B
【解析】试题解析:A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为,不符合题意;
B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率是,符合题意;
C、抛一个质地均匀的正六面体骰子,向上的面点数是5的概率为,不符合题意;
D、抛一枚硬币,出现反面的概率为,不符合题意,
故选B.
B
【解析】试题解析:A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为,不符合题意;
B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率是,符合题意;
C、抛一个质地均匀的正六面体骰子,向上的面点数是5的概率为,不符合题意;
D、抛一枚硬币,出现反面的概率为,不符合题意,
故选B. 已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
A. △ABC的边AB的垂直平分线 B. ∠ACB的平分线所在的直线
C. △ABC的边BC上的中线所在的直线 D. △ABC的边AC上的高所在的直线
 C
【解析】根据条件可以推出AB=AC,由此即可判断.
【解析】
∵l=AB+BC+AC,
∴BC=l?2AB=AB+BC+AC?2AB,
∴AB=AC,
∴△ABC中BC边中线所在的直线是△ABC的对称轴.
故选C.
C
【解析】根据条件可以推出AB=AC,由此即可判断.
【解析】
∵l=AB+BC+AC,
∴BC=l?2AB=AB+BC+AC?2AB,
∴AB=AC,
∴△ABC中BC边中线所在的直线是△ABC的对称轴.
故选C. 
