题目内容
一个角的余角比这个角的补角小_____.
90°
【解析】设这个角是x°，由题意得
（180°- x°）-（90°- x°）=90°.
练习册系列答案
相关题目
已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
A. △ABC的边AB的垂直平分线 B. ∠ACB的平分线所在的直线
C. △ABC的边BC上的中线所在的直线 D. △ABC的边AC上的高所在的直线
C
【解析】根据条件可以推出AB=AC，由此即可判断．
【解析】
∵l=AB+BC+AC，
∴BC=l?2AB=AB+BC+AC?2AB，
∴AB=AC，
∴△ABC中BC边中线所在的直线是△ABC的对称轴.
故选C. 在Rt△ABC中，∠C＝90°，下列说法正确的有( )
①sinA＞cosA ②sin2A＋cos2A＝1 ③tanA·tanB＝1 ④tanA＝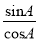
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
B
【解析】∵∠C=90°，∴，已知中不知BC与AC在大小关系，故①错误；
，故②正确；
，故③正确；
，故④正确，
故选B. 如果∠1与∠2互补，∠1与∠3互余，那么 ( )
A. ∠2＞∠3 B. ∠2=∠3 C. ∠2＜∠3 D. ∠2≥∠3
A
【解析】∵∠1与∠2互补，∴∠1+∠2=180°，
∵∠1与∠3互余，∴∠1+∠3=90°，
∴∠1+∠2-（∠1+∠3）=180°-90°，
∴∠2-∠3=90°，
∴∠2＞∠3．
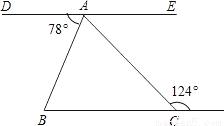
故选A． 如图,DAE是一条直线,DE∥BC，则∠BAC=___度.
46°．
【解析】试题分析：∵DE∥BC，∴∠DAC=124°，∴∠BAC=∠DAC﹣∠DAB=124°﹣78°=46°．故答案为：46°． 两条直线相交，有_____对对顶角，三条直线两两相交，有_____对对顶角.
两 六
【解析】两条直线相交，有两对对顶角，三条直线两两相交，有六对对顶角. 已知△ABC关于直线MN对称，则下列说法错误的是（ ）
A. △ABC中必有一个顶点在直线MN上
B. △ABC中必有两个角相等
C. △ABC中，必有两条边相等
D. △ABC中必有有一个角等于60°
D
【解析】【解析】
∵△ABC关于直线MN对称，∴△ABC为等腰三角形，其对称轴为底边上的高所在的直线．
A、△ABC中必有一个顶点在直线MN上，故本选项正确；
B、△ABC中必有两个角相等，故本选项正确；
C、△ABC中，必有两条边相等，故本选项正确；
D、当该等腰三角形是等边三角形时，△ABC中有一个角等于60°，故本选项错误．
故选D． 计算:(0.125)2 018×(22 018)3=___________.
1
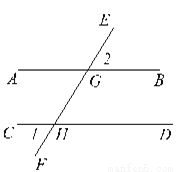
【解析】原式=(0.125)2 018×82 018=(0.125×8)2 018=1. 已知：如图，直线EF与AB、CD分别相交于点G、H，∠1=∠3。
求证：AB∥CD。
证明见解析
【解析】试题分析：首先根据对顶角的性质得出∠AGH=∠GHD，最后根据内错角相等两直线平行得出答案．
试题解析：∵∠1=∠GHD，∠3=∠AGH（对顶角相等），∠1=∠3（已知），∴∠AGH=∠GHD，
∴AB∥CD（内错角相等，内错角相等）．