Question

5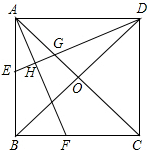．已知，如图，在正方形ABCD中，O是对角线的交点，AF平分∠BAC，DH⊥AF于点H，交AC于点G，DH延长线交AB于点E．
求证：BE=2OG．

Answer 1

分析 作OM∥AB交DE于M．首先证明OM是△DEB的中位线，再证明OG=OM即可解决问题．

解答 解：作OM∥AB交DE于M．

∵四边形ABCD是正方形，
∴OB=OD，
∵OH∥BE，
∴EM=DM，
∴BE=2OM，
∵∠OAD=∠ADO=∠BAC=45°，
∵FA平分∠BAC，
∴∠EAH=22.5°，
∵AF⊥DE，
∴∠AHE=∠AHD=90°，
∴∠AEH=67.5°，
∵∠ADE+∠AED=90°，
∴∠ADE=22.5°，
∴∠OGD=∠GAD+∠ADE=67.5°，
∵∠AEH=∠OME=67.5°，
∴∠OGM=∠OMG，
∴OG=OM，
∴BE=2OG．

点评 本题考查正方形的性质、三角形的中位线定理、角平分线的定义、等腰三角形的判定和性质等知识，解题的关键是学会添加辅助线，构造三角形中位线解决问题，属于中考常考题型．