题目内容
6.(1)$\frac{1-x}{3}$≤$\frac{1-2x}{7}$(2)$\left\{\begin{array}{l}{5x-6≤2(x+3)}\\{\frac{x}{4}-1<\frac{x-3}{3}}\end{array}\right.$.
分析 (1)先去分母,再去括号,移项,合并同类项,把x的系数化为1即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)去分母得,7(1-x)≤3(1-2x),
去括号得,7-7x≤3-6x,
移项得,-7x+6x≤3-7,
合并同类项得,-x≤-1,
x的系数化为1得,x≥1;
(2)$\left\{\begin{array}{l}{5x-6≤2(x+3)①}\\{\frac{x}{4}-1<\frac{x-3}{3}②}\end{array}\right.$,由①得,x≤4,由②得,x>0,
故不等式组的解集为:0<x≤4.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键

练习册系列答案
相关题目
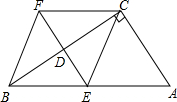 如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE
如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE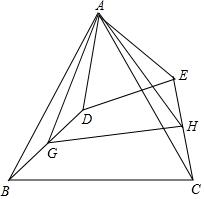 如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.
如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.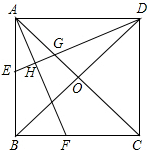 已知,如图,在正方形ABCD中,O是对角线的交点,AF平分∠BAC,DH⊥AF于点H,交AC于点G,DH延长线交AB于点E.
已知,如图,在正方形ABCD中,O是对角线的交点,AF平分∠BAC,DH⊥AF于点H,交AC于点G,DH延长线交AB于点E.