题目内容
19.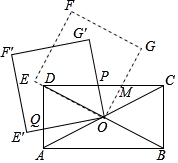 如图,矩形ABCD的对角线交于点O,正方形OEFG的一条边OE在直线OD上,OG与CD交于点M,正方形OEFG绕点O逆时针旋转,OG′,OE′分别与CD,AD交于点P,Q.已知矩形长与宽的比值为2,则在旋转过程中PM:DQ=( )
如图,矩形ABCD的对角线交于点O,正方形OEFG的一条边OE在直线OD上,OG与CD交于点M,正方形OEFG绕点O逆时针旋转,OG′,OE′分别与CD,AD交于点P,Q.已知矩形长与宽的比值为2,则在旋转过程中PM:DQ=( )| A. | 1:3 | B. | 2:3 | C. | 1:2 | D. | 3:4 |
分析 由旋转的性质得∠MOP=∠DOQ,根据余角的性质得到∠PMO=∠QDO,根据相似三角形的性质得到$\frac{PM}{DQ}=\frac{OM}{OD}$,根据三角函数的定义 得到$\frac{OM}{OD}$=$\frac{AD}{AB}$=$\frac{1}{2}$,于是得到结论.
解答  解:由旋转的性质得∠MOP=∠DOQ,
解:由旋转的性质得∠MOP=∠DOQ,
∵∠DMO+∠MDO=∠MDO+∠QDO=90°,
∴∠PMO=∠QDO,
∴△OPM∽△DOQ,
∴$\frac{PM}{DQ}=\frac{OM}{OD}$,
∵CD∥AB,
∴∠MDO=∠ABD,
∴tan∠MDO=tan∠ABD,
即$\frac{OM}{OD}$=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴PM:DQ=$\frac{1}{2}$,
故选C.
点评 本题考查了旋转的性质相似三角形的判定和性质,三角函数的定义,正方形的性质矩形的性质,熟练掌握各定理是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
9.若a-b=2,则a2-b2-4b的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
10. 如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
 如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )| A. | m=n | B. | m>n | ||
| C. | m<n | D. | m、n的大小关系不确定 |
9.在数1、2、3和4中,是方程x2+x-12=0的根的为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
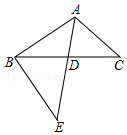 如图,△ABC中,AE交BC于点D,∠CAE=∠CBE,AD:DE=3:5,AE=16,BD=8,则DC的长等于$\frac{15}{2}$.
如图,△ABC中,AE交BC于点D,∠CAE=∠CBE,AD:DE=3:5,AE=16,BD=8,则DC的长等于$\frac{15}{2}$.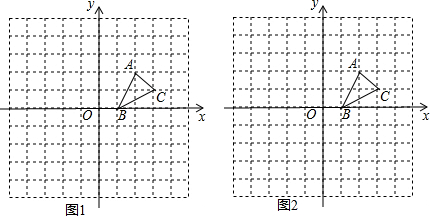
 补全解题过程.
补全解题过程.