题目内容
7.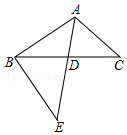 如图,△ABC中,AE交BC于点D,∠CAE=∠CBE,AD:DE=3:5,AE=16,BD=8,则DC的长等于$\frac{15}{2}$.
如图,△ABC中,AE交BC于点D,∠CAE=∠CBE,AD:DE=3:5,AE=16,BD=8,则DC的长等于$\frac{15}{2}$.
分析 证明三角形相似得出比例式,即可解决问题.
解答 解:∵AD:DE=3:5,AE=16,
∴DE=10,AD=6,
∵∠CAE=∠CBE,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴$\frac{AD}{BD}=\frac{DC}{DE}$,
∴$\frac{6}{8}=\frac{DC}{10}$,
解得:DE=$\frac{15}{2}$;
故答案为:$\frac{15}{2}$,
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定与性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
| A. | 将原三角形向左平移两个单位 | B. | 将原三角形向右平移两个单位 | ||
| C. | 关于x轴对称 | D. | 关于y轴对称 |
15. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 72 | B. | 52 | C. | 80 | D. | 76 |
2.下列命题中,假命题的是( )
| A. | 分别有一个角是110°的两个等腰三角形相似 | |
| B. | 如果两个三角形相似,则他们的面积比等于相似比 | |
| C. | 若5x=8y,则$\frac{x}{y}$=$\frac{8}{5}$ | |
| D. | 有一个角相等的两个菱形相似 |
19.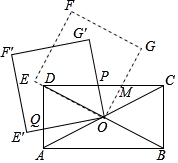 如图,矩形ABCD的对角线交于点O,正方形OEFG的一条边OE在直线OD上,OG与CD交于点M,正方形OEFG绕点O逆时针旋转,OG′,OE′分别与CD,AD交于点P,Q.已知矩形长与宽的比值为2,则在旋转过程中PM:DQ=( )
如图,矩形ABCD的对角线交于点O,正方形OEFG的一条边OE在直线OD上,OG与CD交于点M,正方形OEFG绕点O逆时针旋转,OG′,OE′分别与CD,AD交于点P,Q.已知矩形长与宽的比值为2,则在旋转过程中PM:DQ=( )
 如图,矩形ABCD的对角线交于点O,正方形OEFG的一条边OE在直线OD上,OG与CD交于点M,正方形OEFG绕点O逆时针旋转,OG′,OE′分别与CD,AD交于点P,Q.已知矩形长与宽的比值为2,则在旋转过程中PM:DQ=( )
如图,矩形ABCD的对角线交于点O,正方形OEFG的一条边OE在直线OD上,OG与CD交于点M,正方形OEFG绕点O逆时针旋转,OG′,OE′分别与CD,AD交于点P,Q.已知矩形长与宽的比值为2,则在旋转过程中PM:DQ=( )| A. | 1:3 | B. | 2:3 | C. | 1:2 | D. | 3:4 |
16.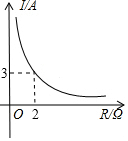 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )| A. | $I=\frac{3}{R}$ | B. | $I=-\frac{6}{R}$ | C. | $I=-\frac{3}{R}$ | D. | $I=\frac{6}{R}$ |
 如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有①②③④.(请填序号)
如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有①②③④.(请填序号) 如图,甲、乙两个转盘转动一次,最终指针指向红色区域是(填“是”或“不是”)等可能性事件.
如图,甲、乙两个转盘转动一次,最终指针指向红色区域是(填“是”或“不是”)等可能性事件.