题目内容
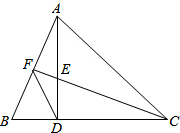 如图,在△ABC中,∠ACB=45°,AD是△ABC的高,在AD上取点E,使得DE=DB,连接CE并延长,交边AB于点F,连接DF.
如图,在△ABC中,∠ACB=45°,AD是△ABC的高,在AD上取点E,使得DE=DB,连接CE并延长,交边AB于点F,连接DF.(1)求证:AB=CE;
(2)求证:BF+EF=
| 2 |
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据三角形高线的定义求出∠ADB=∠CDE=90°,并判断出△ACD是等腰直角三角形,根据等腰直角三角形的性质可得AD=CD,然后利用“边角边”证明△ABD和△CED全等,根据全等三角形对应边相等可得AB=CE;
(2)在EC上截取EG=BF,根据全等三角形对应角相等可得∠B=∠CED,然后利用“边角边”证明△BDF和△EDG全等,根据全等三角形对应边相等可得DF=DG,全等三角形对应角相等可得∠BDF=∠EDG,再求出∠FDG=90°,判断出△DFG是等腰直角三角形,然后根据等腰直角三角形的性质证明即可.
(2)在EC上截取EG=BF,根据全等三角形对应角相等可得∠B=∠CED,然后利用“边角边”证明△BDF和△EDG全等,根据全等三角形对应边相等可得DF=DG,全等三角形对应角相等可得∠BDF=∠EDG,再求出∠FDG=90°,判断出△DFG是等腰直角三角形,然后根据等腰直角三角形的性质证明即可.
解答:证明:(1)∵AD是△ABC的高,∠ACB=45°,
∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,
∴AD=CD,
在△ABD和△CED中,
,
∴△ABD≌△CED(SAS),
∴AB=CE;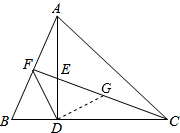
(2)如图,在EC上截取EG=BF,
∵△ABD≌△CED,
∴∠B=∠CED,
在△BDF和△EDG中,
,
∴△BDF≌△EDG(SAS),
∴DF=DG,∠BDF=∠EDG,
∴∠FDG=∠FDE+∠EDG=∠FDE+∠BDF=∠ADB=90°,
∴△DFG是等腰直角三角形,
∴BF+EF=EG+EF=FG=
FD,
故BF+EF=
FD.
∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,
∴AD=CD,
在△ABD和△CED中,
|
∴△ABD≌△CED(SAS),
∴AB=CE;

(2)如图,在EC上截取EG=BF,
∵△ABD≌△CED,
∴∠B=∠CED,
在△BDF和△EDG中,
|
∴△BDF≌△EDG(SAS),
∴DF=DG,∠BDF=∠EDG,
∴∠FDG=∠FDE+∠EDG=∠FDE+∠BDF=∠ADB=90°,
∴△DFG是等腰直角三角形,
∴BF+EF=EG+EF=FG=
| 2 |
故BF+EF=
| 2 |
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,难点在于(2)作辅助线构造成全等三角形和等腰直角三角形.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目

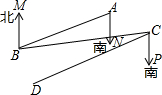 已知:如图B处在A处的南偏西60°方向,C处在B处的北偏东80°方向.
已知:如图B处在A处的南偏西60°方向,C处在B处的北偏东80°方向. 如图,D是Rt△ABC的斜边AB的中点,E是BC上的一点,且BE=
如图,D是Rt△ABC的斜边AB的中点,E是BC上的一点,且BE=