题目内容
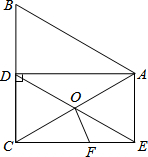 如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为4的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
考点:矩形的判定与性质,等边三角形的性质
专题:
分析:(1)根据平行四边形判定得出平行四边形,再根据矩形判定推出即可;
(2)分别求出AE、OH、CE、CF的长,再求出三角形AEC和三角形COF的面积,即可求出答案.
(2)分别求出AE、OH、CE、CF的长,再求出三角形AEC和三角形COF的面积,即可求出答案.
解答:(1)证明:∵CE∥AD且CE=AD,
∴四边形ADCE是平行四边形,
∵在△ABC中,AB=AC,AD平分∠BAC,
∴AD⊥BC(等腰三角形三线合一性质),
∴∠ADC=90°,
∴四边形ADCE是矩形;

(2)解:∵△ABC是等边三角形,边长为4,
∴AC=4,∠DAC=30°,
∴∠ACE=30°,AE=2,CE=2
,
∵四边形ADCE为矩形,
∴OC=OA=2,
∵CF=CO,
∴CF=2,
过O作OH⊥CE于H,
∴OH=
OC=1,
∴S四边形AOFE=S△AEC-S△COF=
×2×2
-
×2×1=2
-1.
∴四边形ADCE是平行四边形,
∵在△ABC中,AB=AC,AD平分∠BAC,
∴AD⊥BC(等腰三角形三线合一性质),
∴∠ADC=90°,
∴四边形ADCE是矩形;

(2)解:∵△ABC是等边三角形,边长为4,
∴AC=4,∠DAC=30°,
∴∠ACE=30°,AE=2,CE=2
| 3 |
∵四边形ADCE为矩形,
∴OC=OA=2,
∵CF=CO,
∴CF=2,
过O作OH⊥CE于H,
∴OH=
| 1 |
| 2 |
∴S四边形AOFE=S△AEC-S△COF=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
点评:本题考查了矩形的性质和判定,等边三角形的性质,含30度角的直角三角形性质,勾股定理等知识点的应用,题目是一道综合性比较强的题目,难度适中.

练习册系列答案
相关题目
 如图,是一储水容器,当水从上方倒入容器(每秒倒入的水量相同)中时,水位高度h与倒水时间t的函数图象是( )
如图,是一储水容器,当水从上方倒入容器(每秒倒入的水量相同)中时,水位高度h与倒水时间t的函数图象是( )



 如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=



 如图,点C、F在BE上,BF=CE,AB=DE,∠B=∠E.求证:∠ACE=∠DFE.
如图,点C、F在BE上,BF=CE,AB=DE,∠B=∠E.求证:∠ACE=∠DFE.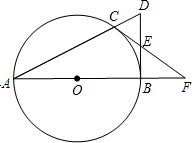 如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证:
如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证: