题目内容
10.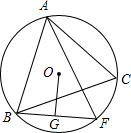 已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.
已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.
分析 作直径FM,连结BM、AM,根据圆周角定理得到∠MAF=90°,根据三角形中位线定理得到OG=$\frac{1}{2}$BM,根据题意得到MA∥BC,根据平行线的性质得到结论.
解答 证明:如图,作直径FM,连结BM、AM,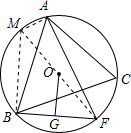
则∠MAF=90°,
∵OG⊥BF,
∴BG=GF,
在△FBM中,∵OF=OM,FG=GB,
∴OG=$\frac{1}{2}$BM,又OG=$\frac{1}{2}$AC,
∴BM=AC,
∴MA∥BC,
∴AF⊥BC.
点评 本题考查的是圆周角定理和三角形中位线定理,掌握直径所对的圆周角是直角、三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
5.若不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x+a>0}\end{array}\right.$的解集为2<x≤3,则a,b的值分别为( )
| A. | -2,3 | B. | 2,-3 | C. | 3,-2 | D. | -3,2 |
15.如图(1),B是线段AD上一点,分别以AB、BD为边在AD同侧作等边△ABC和等边△BDE,得到(1)△ABE≌△CBD;(2)AE与CD相交所得的锐角为60°.如图(2),B是线段AE上一点,分别以AB、BE为边在AE同侧作正方形ABCD和正方形BEFG,除了得到△ABG≌△CBE外,AG与CE相交所得的角的度数为( )
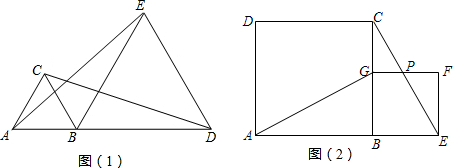

| A. | 90° | B. | 60° | C. | 120° | D. | 不能确定 |
19.函数$y=(m+1){x}^{{m}^{2}+m-1}$是反比例函数,则m的值为( )
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 0或1 |
20.y是x的反比例函数,下表给出了x与y的一些值:
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表.
| x | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 3 | ||
| y | $\frac{2}{3}$ | 2 | -1 |
(2)根据函数表达式完成上表.
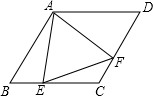 如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F