题目内容
8.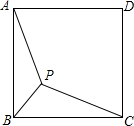 如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.
如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.
分析 先根据正方形的性质得BA=BC,∠ABC=90°,则可把△BAP绕点B顺时针旋转90°得到△CBE,连结PE,如图,根据旋转的性质得BP=BE=2,CE=AP=4,∠PBE=90°,∠BEC=∠APB=135°,于是可判断△PBE为等腰直角三角形,所以PE=$\sqrt{2}$PB=2$\sqrt{2}$,∠PEB=45°,则∠PEC=90°,然后在Rt△PEC中利用勾股定理计算PC的长.
解答 解: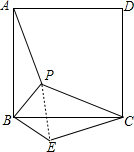 ∵四边形ABCD为正方形,
∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
把△BAP绕点B顺时针旋转90°得到△CBE,连结PE,如图,
∴BP=BE=2,CE=AP=4,∠PBE=90°,∠BEC=∠APB=135°,
∴△PBE为等腰直角三角形,
∴PE=$\sqrt{2}$PB=2$\sqrt{2}$,∠PEB=45°,
∴∠PEC=135°-45°=90°,
在Rt△PEC中,∵PE=2$\sqrt{2}$,CE=4,
∴PC=$\sqrt{{4}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$.
故答案为2$\sqrt{6}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
18.在等腰三角形中,顶角是36°,则底角是( )
| A. | 72° | B. | 36° | C. | 70° | D. | 80° |
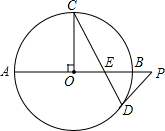 如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.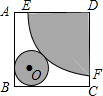 要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.
要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r. 已知:如图,直线AB、CD相交于点O,OE⊥CD于O点,∠AOC=20°,若OF平分∠BOE,求∠DOF.
已知:如图,直线AB、CD相交于点O,OE⊥CD于O点,∠AOC=20°,若OF平分∠BOE,求∠DOF. 如图,在Rt△ABC中,∠ACB=90°,将其绕点A顺时针旋转80°得到△AB′C′,若∠B=30°,则∠CAB′为20°.
如图,在Rt△ABC中,∠ACB=90°,将其绕点A顺时针旋转80°得到△AB′C′,若∠B=30°,则∠CAB′为20°.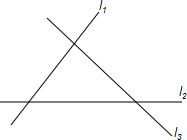 如图所示,直线了l1,l2,l3表示三条相互交叉公路,现要建一个货物中转站,求它到三条公路的距离相等,则可供选择的地址共有( )处.
如图所示,直线了l1,l2,l3表示三条相互交叉公路,现要建一个货物中转站,求它到三条公路的距离相等,则可供选择的地址共有( )处.