题目内容
2.如图1,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点构建平行四边形,求平行四边形的第四个顶点的坐标.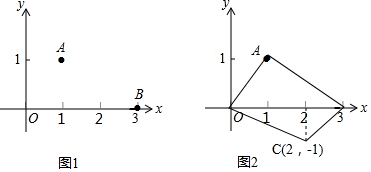
解:连接OA,AB,将线段OA沿A→B平移,使A与B重合,则O与第四个顶点C重合,如图2.
A(1,1)$→_{向下平移1个单位长度}^{向右平移2个单位长度}$B(3,0),则O(0,0)$→_{向下平移1个单位长度}^{向右平移2个单位长度}$C(2,-1).
仿照上述方法,请求出剩下的第四个顶点的坐标.
分析 利用平行四边形的性质、平移变换等知识即可解决问题,注意本题有两解.
解答  解:连接OA,AB,将线段OA沿A→B平移,使O与B重合,则A与第四个顶点C重合,
解:连接OA,AB,将线段OA沿A→B平移,使O与B重合,则A与第四个顶点C重合,
O(0,0)向上平移一个单位,向右平移一个单位得到A(1,1),
B(3,0)向上平移一个单位,向右平移一个单位得到C(4,1),
将线段AB沿A→B平移,使B与O重合,则A与第四个顶点C′重合,
B(3,0),向左平移3个单位得到O(0,0),
A(1,1)向左平移3个单位得到C′(-2,1),
∴剩下的第四个顶点的坐标为(4,1)或(-2,1).
点评 本题考查平行四边形的性质和判定、平移变换等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
4.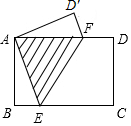 如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE=$\frac{5}{13}$,那么重叠部分△AEF的面积为( )
如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE=$\frac{5}{13}$,那么重叠部分△AEF的面积为( )
 如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE=$\frac{5}{13}$,那么重叠部分△AEF的面积为( )
如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE=$\frac{5}{13}$,那么重叠部分△AEF的面积为( )| A. | $\frac{39}{4}$ | B. | $\frac{39}{8}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
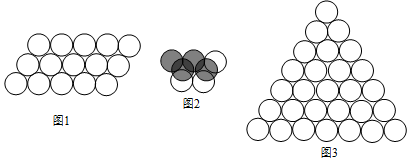
10.五一假期,小明和小华共同设计了一款拼图,他们用乒乓球粘成了下面几种造型的拼板(每种一块,没有重复):
(1)你能用部分拼板拼成图1中的平行四边形吗?所使用的拼板形状不能重复,请在图1中用不同颜色或底纹画出来.
(2)如图2,小华想用拼板摆出一个三棱锥造型,三棱锥的每条棱上有三个乒乓球,他已经用A5和B完成了一部分(图2是从上往下看的样子),请从剩下的拼板中挑出一块完成拼图,你认为需要的拼板是A1.
(3)小明试图用部分拼板拼出图3中的大三角形,请判断他能否成功?如果能,在图3中用不同颜色或底纹画出拼板的摆法;如果不能,请说明理由.
| A组 |  | 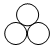 | 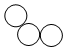 | |||
| A1 | A2 | A3 | ||||
| B组 | 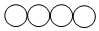 | 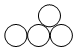 |  |  |  |  |
| B1 | B2 | B3 | B4 | B5 | B6 |
(2)如图2,小华想用拼板摆出一个三棱锥造型,三棱锥的每条棱上有三个乒乓球,他已经用A5和B完成了一部分(图2是从上往下看的样子),请从剩下的拼板中挑出一块完成拼图,你认为需要的拼板是A1.
(3)小明试图用部分拼板拼出图3中的大三角形,请判断他能否成功?如果能,在图3中用不同颜色或底纹画出拼板的摆法;如果不能,请说明理由.

17.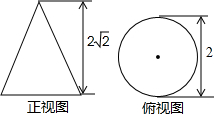 如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
 如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
 如图,若∠1=∠2=∠3=48°,则∠4=132°.
如图,若∠1=∠2=∠3=48°,则∠4=132°.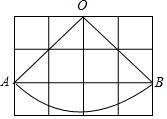 如图,已知小正方形方格的边长为1cm,点O,A,B分别是格点,以O为圆心,OA长为半径作扇形OAB,则弧AB的长为$\sqrt{2}$πcm(结果保留π和根号)
如图,已知小正方形方格的边长为1cm,点O,A,B分别是格点,以O为圆心,OA长为半径作扇形OAB,则弧AB的长为$\sqrt{2}$πcm(结果保留π和根号)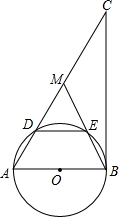 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.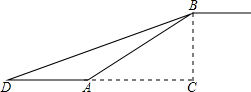 如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).
如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).