题目内容
2. 如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8.
如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8.(1)求反比例函数y=$\frac{k}{x}$的关系式;
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式,并写出t的取值范围.
分析 (1)利用反比例函数的性质直接建立方程求解即可;
(2)根据运动特点用时间表述出BE,BF用就剩下的面积公式即可.
解答 解:(1)∵S△BOC=8,
∴$\frac{1}{2}$|k|=8,
∵k>0,
∴k=16,
∴y=$\frac{16}{k}$.
(2)∵AE=t,
∴BE=4-t
∵BF=2t
∴S=$\frac{1}{2}$BE×BF=$\frac{1}{2}$(4-t)×2t
=-t2+4t(0<t≤2)
点评 此题是反比例函数综合题,主要考查了反比例的性质,动点问题,解本题的关键是熟练反比例函数的性质.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,求AD•BC的值.
如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,求AD•BC的值. 如图,A、B两点分别位于山脚的两端,小明想测量A、B两点间的距离,于是想了个主意:先在地上取一个可以直接达到A、B两点的点C,找到AC、BC的中点D、E,并且测出DE的长为15m,则A、B两点间的距离为30m.
如图,A、B两点分别位于山脚的两端,小明想测量A、B两点间的距离,于是想了个主意:先在地上取一个可以直接达到A、B两点的点C,找到AC、BC的中点D、E,并且测出DE的长为15m,则A、B两点间的距离为30m.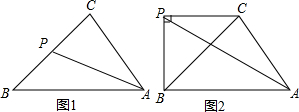
 已知:如图,AD=BC,AC=BD,试证明:∠CAD=∠DBC.
已知:如图,AD=BC,AC=BD,试证明:∠CAD=∠DBC.