题目内容
20.先化简,再求值:($\frac{x^2}{x-2}$+$\frac{4}{2-x}$)÷$\frac{{{x^2}+4x+4}}{x}$.其中x是0,1,2这三个数中合适的数.分析 这是个分式除法与加法混合运算题,运算顺序是先做括号内的减法,此时要注意把各分母先因式分解,确定最简公分母进行通分;做除法时要注意先把除法运算转化为乘法运算,而做乘法运算时要注意先把分子、分母能因式分解的先分解,然后约分.x取不0和2的任何数.
解答 解:($\frac{x^2}{x-2}$+$\frac{4}{2-x}$)÷$\frac{{{x^2}+4x+4}}{x}$
=$\frac{{x}^{2}-4}{x-2}$÷$\frac{{{x^2}+4x+4}}{x}$
=(x+2)•$\frac{x}{(x+2)^{2}}$
=$\frac{x}{x+2}$
当x=1时,原式=$\frac{1}{1+2}$=$\frac{1}{3}$.
点评 本题考查了分式的化简求值.注意:取喜爱的数代入求值时,要特注意原式及化简过程中的每一步都有意义.如果取x=0和2,则原式没有意义,

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
2.把方程$\frac{0.2x-1}{0.3}$-2=$\frac{0.1x-0.7}{0.5}$的分母化为整数的方程是( )
| A. | $\frac{2x-10}{3}$-20=$\frac{x-7}{5}$ | B. | $\frac{2x-10}{3}$-2=$\frac{x-7}{5}$ | C. | $\frac{2x-1}{3}$-2=$\frac{x-7}{5}$ | D. | $\frac{2x-1}{3}$-20=$\frac{x-7}{5}$ |
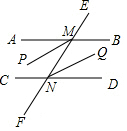 已知:如图,AB∥CD,AB,CD与直线EF分别相交于点M和N,MP平分∠AMF,NQ平分∠DNE.求证:MP∥NQ.
已知:如图,AB∥CD,AB,CD与直线EF分别相交于点M和N,MP平分∠AMF,NQ平分∠DNE.求证:MP∥NQ.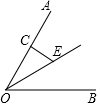 如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$.
如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$.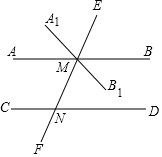 (1)完成下面的证明.
(1)完成下面的证明.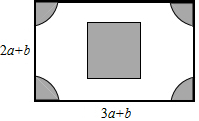 如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.