题目内容
11.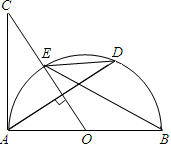 如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.
如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.(1)求证:AC是半⊙O的切线;
(2)若AC=8,cos∠BED=$\frac{4}{5}$,求线段AD的长.
分析 (1)根据OC⊥AD,可得∠AOC+∠2=90°,然后根据∠BED=∠C,证明∠AOC+∠C=90°,据此即可证得C是圆O的切线;
(2)在直角△AOC中利用三角函数和勾股定理求得OC和OA的长度,然后利用三角形的面积公式求得AF的长,再根据垂径定理求解.
解答 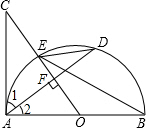 解:(1)AC与圆O相切.证明如下:
解:(1)AC与圆O相切.证明如下:
∵OC⊥AD,
∴∠AOC+∠2=90°
∵∠C=∠BED=∠2,
∴∠AOC+∠C=90°,即∠CAO=90°,
∴AC与⊙O相切;
(2)∵∠BED=∠C,
∴直角△AOC中,cosC=$\frac{AC}{OC}$=cos∠BED=$\frac{4}{5}$,
∴OC=$\frac{AC}{cos∠C}$=$\frac{8}{\frac{4}{5}}$=10,
∴AO=$\sqrt{O{C}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
又∵S△AOC=$\frac{1}{2}$AC•OA=$\frac{1}{2}$OC•AF,
∴AF=$\frac{AC•OA}{OC}$=$\frac{8×6}{10}$=$\frac{24}{5}$,
∵OC⊥AD,
∴AC=2AF=$\frac{48}{5}$.
点评 本题考查了切线的判定以及垂径定理,利用三角形的面积公式求得AF的长是关键.

练习册系列答案
相关题目




 随着生活水平的提高,人们的健康意识、环保意识都在逐步增强,锻炼形式多种多样,跑步、打拳、徒步、广场舞、球类等等,李叔叔每天上班都坚持骑自行车,如图是他从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
随着生活水平的提高,人们的健康意识、环保意识都在逐步增强,锻炼形式多种多样,跑步、打拳、徒步、广场舞、球类等等,李叔叔每天上班都坚持骑自行车,如图是他从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线左侧部分的面积即为t分钟内王叔叔行进的路程s(米).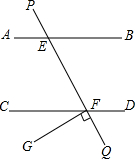 如图,AB∥CD,直线PQ分别交AB、CD于E、F,FG⊥PQ,若∠PEB=130°,求∠CFG的度数.
如图,AB∥CD,直线PQ分别交AB、CD于E、F,FG⊥PQ,若∠PEB=130°,求∠CFG的度数.
 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,∠B=40°,则∠EAF等于40度.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,∠B=40°,则∠EAF等于40度.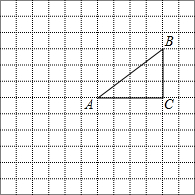 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB′C′. 小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:
小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件: