题目内容
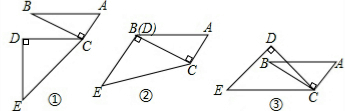
16.在一副三角板ABC和DEF中.(1)当AB∥CD,如图①,求∠DCB的度数.
(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由.
(3)如图③,当∠DCB等于多少度时,AB∥EC?
分析 (1)根据“两直线平行,内错角相等”结合三角板角的特点即可得出结论;
(2)根据三角板角的特点可得出DE⊥CD,AC⊥BC,再根据“垂直于同一直线的两直线平行”即可得出结论;
(3)根据“两直线平行,内错角相等”即可得出∠ABC=∠BCE,再根据三角板角的特点通过角的计算即可得出结论.
解答 解:(1)∵AB∥CD,
∴∠DCB=∠ABC=30°.
(2)DE∥AC.理由如下:
∵∠CDE=∠ACB=90°,
∴DE⊥CD,AC⊥BC,
∵CD与CB重合,
∴DE⊥BC,AC⊥BC,
∴DE∥AC.
(3)∵AB∥EC,
∴∠ABC=∠BCE=30°,
又∵∠DCE=45°,
∴∠DCB=∠DCE-∠BCE=15°.
故当∠DCB等于15度时,AB∥EC.
点评 本题考查了平行线的判定与性质,解题的关键是:(1)找出∠DCB=∠ABC;(2)找出DE⊥BC,AC⊥BC;(3)找出∠ABC=∠BCE.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
6.点A在平面直角坐标系中的第四象限,且点A到x轴的距离为1,到y轴的距离为3,则A的坐标为( )
| A. | (-3,1) | B. | (3,-1) | C. | (-1,3) | D. | (1,-3) |
8.下列图中∠1和∠2是同位角的是( )


| A. | ①、②、③ | B. | ②、③、④ | C. | ③、④、⑤ | D. | ①、②、⑤ |
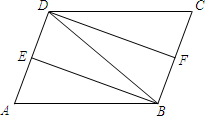 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.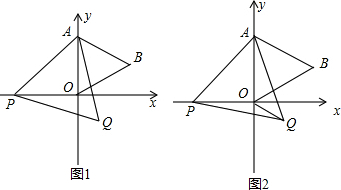
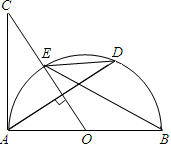 如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.
如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.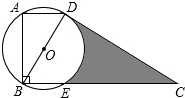 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=$\sqrt{3}$,CD=6,以对角线BD为直径作⊙O与CD交于点D,与BC交于点E,且∠ABD为30°.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=$\sqrt{3}$,CD=6,以对角线BD为直径作⊙O与CD交于点D,与BC交于点E,且∠ABD为30°. 如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.
如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.