题目内容
1. 小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:
小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:①AB=BC,
②∠ABC=90°,
③AC=BD,
④AC⊥BD
中选两个作为补充条件,使?ABCD为正方形(如图所示),现有如下四种选法,你认为其中错误的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
分析 利用矩形、菱形、正方形之间的关系与区别,结合正方形的判定方法分别判断得出即可.
解答 解:A、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
C、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;
D、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.
故选:C.
点评 此题主要考查了正方形的判定以及矩形、菱形的判定方法,正确掌握正方形的判定方法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
 已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
9. 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )| A. | AB=CD | B. | AO=CO | C. | AC=BD | D. | BO=DO |
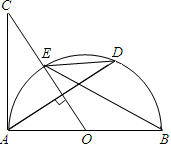 如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.
如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C. 如图,在?ABCD中,BE平分∠ABC,∠D=80°,则∠AEB=40°.
如图,在?ABCD中,BE平分∠ABC,∠D=80°,则∠AEB=40°. 如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.
如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:BE=DF(答案不唯一);.