题目内容
3. 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,∠B=40°,则∠EAF等于40度.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,∠B=40°,则∠EAF等于40度.
分析 由在平行四边形ABCD中,∠B=40°,即可求得∠D与∠BAD的度数,然后由AE⊥BC,AF⊥CD,即可求得∠BAE与∠DAF的度数,继而求得答案.
解答 解:∵在平行四边形ABCD中,∠B=40°,
∴∠D=∠B=40°,∠BAD=180°-∠B=140°,
∵AE⊥BC,AF⊥CD,
∴∠BAE=90°-∠B=50°,∠DAF=90°-∠D=50°,
∴∠EAF=∠BAD-∠BAE-∠DAF=40°.
故答案为:40.
点评 此题考查了平行四边形的性质.注意根据平行四边形的对角相等求得∠D的度数是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列图中∠1和∠2是同位角的是( )


| A. | ①、②、③ | B. | ②、③、④ | C. | ③、④、⑤ | D. | ①、②、⑤ |
12. 已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
 已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
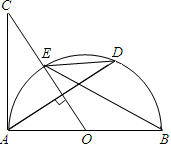 如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.
如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.