题目内容
9.计算:(2-$\sqrt{3}$+$\sqrt{5}$)2-(2+$\sqrt{3}$-$\sqrt{5}$)2.分析 先利用平方差公式得到原式=(2-$\sqrt{3}$+$\sqrt{5}$+2+$\sqrt{3}$-$\sqrt{5}$)(2-$\sqrt{3}$+$\sqrt{5}$-2-$\sqrt{3}$+$\sqrt{5}$),然后把括号内合并后进行二次根式的乘法运算.
解答 解:原式=(2-$\sqrt{3}$+$\sqrt{5}$+2+$\sqrt{3}$-$\sqrt{5}$)(2-$\sqrt{3}$+$\sqrt{5}$-2-$\sqrt{3}$+$\sqrt{5}$)
=4×(2$\sqrt{5}$-2$\sqrt{3}$)
=8$\sqrt{5}$-8$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
19.若二次根式$\sqrt{2x-4}$有意义,则x的取值范围是( )
| A. | x=2 | B. | x≠2 | C. | x≤2 | D. | x≥2 |
14.在平面直角坐标系中,已知O是原点,四边形ABCD是长方形,A,B,C的坐标分别为A(-3,1),B(-3,3),C(2,3).
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
(3)平移(2)中长方形ABCD,几秒钟后△OBD的面积等于长方形ABCD的面积.
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 |
19.为了了解某校七年级考数学科各分数段成绩分布情况,从中抽取200名考生的段考数学成绩进行统计分析,在这个问题中,样本是( )
| A. | 200 | |
| B. | 被抽取的200名学生 | |
| C. | 被抽取的200名考生的段考数学成绩 | |
| D. | 某校七年级段考数学成绩 |
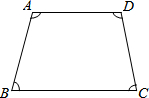 多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.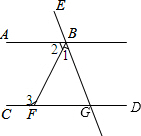 如图,已知AB∥CD,∠1:∠2=1:2,∠2:∠3=2:3,求∠1、∠2、∠3的度数.
如图,已知AB∥CD,∠1:∠2=1:2,∠2:∠3=2:3,求∠1、∠2、∠3的度数.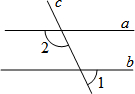 如图,直线c与a、b都相交,a∥b,如果∠2=110°,那么∠1=70°.
如图,直线c与a、b都相交,a∥b,如果∠2=110°,那么∠1=70°.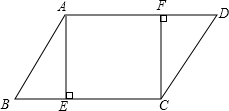 如图所示,在四边形ABCD中,AE⊥BC于E,CF⊥AD于F,如果AD∥BC且AF=CE,那么四边形AECF是平行四边形?说明理由.
如图所示,在四边形ABCD中,AE⊥BC于E,CF⊥AD于F,如果AD∥BC且AF=CE,那么四边形AECF是平行四边形?说明理由.