题目内容
6.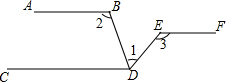 如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.
如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.
分析 先根据CD∥EF得出∠3=∠1+∠BDC,再由AB∥CD得出∠BCD=180°-∠2,由此可得出结论.
解答 解:∠3+∠2-∠1=180°.
理由:∵CD∥EF,
∴∠3=∠1+∠BDC.
∵AB∥CD,
∴∠BCD=180°-∠2,
∴∠3=∠1+180°-∠2,即∠3+∠2-∠1=180°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等,同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在平面直角坐标系中,已知O是原点,四边形ABCD是长方形,A,B,C的坐标分别为A(-3,1),B(-3,3),C(2,3).
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
(3)平移(2)中长方形ABCD,几秒钟后△OBD的面积等于长方形ABCD的面积.
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 |
11.实验学校计划阻值共青团员372人到某爱国主义基地接受教育,并安排8位老师同行,经学校与汽车出租公司协商,有两种型号客车可供选择,它们的载客量和租金如表所示,为了保证每人都有座位,学校决定租8辆车.
(1)写出符合要求的租车方案,并说明理由;
(2)设租甲种客车x辆,总租金共y(元),写出y与x之间的函数关系式;
(3)在(1)的方案中,求出租金最少的租车方案.
(1)写出符合要求的租车方案,并说明理由;
(2)设租甲种客车x辆,总租金共y(元),写出y与x之间的函数关系式;
(3)在(1)的方案中,求出租金最少的租车方案.
| 车种 人数与租金 单位 | 甲种客车 | 乙种客车 |
| 载客量(单位:人/辆) | 50 | 30 |
| 租金(单位:元/辆) | 400 | 200 |
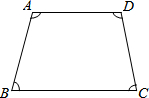 多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.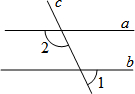 如图,直线c与a、b都相交,a∥b,如果∠2=110°,那么∠1=70°.
如图,直线c与a、b都相交,a∥b,如果∠2=110°,那么∠1=70°.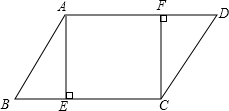 如图所示,在四边形ABCD中,AE⊥BC于E,CF⊥AD于F,如果AD∥BC且AF=CE,那么四边形AECF是平行四边形?说明理由.
如图所示,在四边形ABCD中,AE⊥BC于E,CF⊥AD于F,如果AD∥BC且AF=CE,那么四边形AECF是平行四边形?说明理由.