题目内容
 我们把两相邻边分别相等的四边形叫做“筝形”.如图,在筝形ABCD中,AB=AD,BC=DC,AC、BD相交于点O.
我们把两相邻边分别相等的四边形叫做“筝形”.如图,在筝形ABCD中,AB=AD,BC=DC,AC、BD相交于点O.(1)求证:OB=OD;
(2)若AC=6,BD=4,求筝形ABCD的面积.
考点:全等三角形的判定与性质
专题:新定义
分析:(1)易证△ABC≌△ADC,可得∠BAO=∠DAO,即可证明△BAO≌△DAO,即可求得BO=DO;
(2)根据△BAO≌△DAO可得∠AOB=∠AOD=90°,再根据筝形ABCD的面积=S△ACB+S△ACD即可解题.
(2)根据△BAO≌△DAO可得∠AOB=∠AOD=90°,再根据筝形ABCD的面积=S△ACB+S△ACD即可解题.
解答:(1)证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC,(SSS)
∴∠BAO=∠DAO,
在△BAO和△DAO中,
,
∴△BAO≌△DAO(SAS),
∴BO=DO;
(2)解:∵△BAO≌△DAO,
∴∠AOB=∠AOD=90°,
∴筝形ABCD的面积=S△ACB+S△ACD
=
AC•BO+
AC•DO=
AC•(BO+DO)
=
AC•BD
=12.
|
∴△ABC≌△ADC,(SSS)
∴∠BAO=∠DAO,
在△BAO和△DAO中,
|
∴△BAO≌△DAO(SAS),
∴BO=DO;
(2)解:∵△BAO≌△DAO,
∴∠AOB=∠AOD=90°,
∴筝形ABCD的面积=S△ACB+S△ACD
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=12.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质,本题中求证△BAO≌△DAO是解题的关键.

练习册系列答案
相关题目
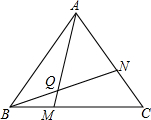 老师布置了一道思考题:
老师布置了一道思考题: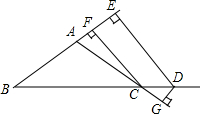 如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系.
如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系. 如图,在△ABC中∠BAC=62°,现将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点在同一条线上,那么旋转角的度数为
如图,在△ABC中∠BAC=62°,现将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点在同一条线上,那么旋转角的度数为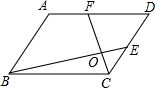 如图,平行四边形ABCD中,F为AD中点,CO=
如图,平行四边形ABCD中,F为AD中点,CO=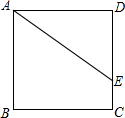 如图,正方形ABCD的面积为3,点E是DC边上一点,DE=1,将线段AE绕点A旋转,使点E落在直线BC上,落点记为F,则∠EAF=
如图,正方形ABCD的面积为3,点E是DC边上一点,DE=1,将线段AE绕点A旋转,使点E落在直线BC上,落点记为F,则∠EAF= 在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(-2,3),D(4,3),并将各点用线段依次连接构成一个四边形ABCD.
在平面直角坐标系中描出下列各点A(2,1),B(0,1),C(-2,3),D(4,3),并将各点用线段依次连接构成一个四边形ABCD. 如图所示:若∠CDE=26°,求∠C的度数.
如图所示:若∠CDE=26°,求∠C的度数.