题目内容
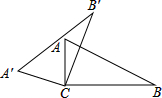如图，将Rt△ABC绕C点逆时针旋转得到△A′B′C′，若∠A′BC=160°，则此图形旋转角是考点：旋转的性质
专题：
分析：由旋转的性质可知△ABC≌△A′B′C′，所以BC=B′C′，所以∠BCB′为旋转角，再根据已知条件即可求出∠BCB′的度数，问题得解．
解答：解：∵将Rt△ABC绕C点逆时针旋转得到△A′B′C′，
∴△ABC≌△A′B′C′，
∴BC=B′C′，∠ACB′=∠ACB=90°，
∴∠BCB′为旋转角，
∵∠ACB′=∠ACB=90°，∠A′CB=160°，
∴∠B′CB=70°，
∴此图形旋转角是70°，
故答案为：70．
∴△ABC≌△A′B′C′，
∴BC=B′C′，∠ACB′=∠ACB=90°，
∴∠BCB′为旋转角，
∵∠ACB′=∠ACB=90°，∠A′CB=160°，
∴∠B′CB=70°，
∴此图形旋转角是70°，
故答案为：70．
点评：本题考查旋转的性质：旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．要注意旋转的三要素：①定点--旋转中心；②旋转方向；③旋转角度．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图，在等腰Rt△ABC中，∠ABC=90°，AB=BC，D为斜边AC延长线上一点，过D点作BC的垂线交其延长线于点E，在AB的延长线上取一点F，使得BF=CE，连接EF．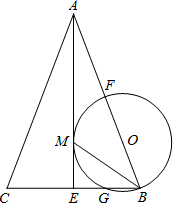
如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．
如图，在?ABCD中，∠A=70°，将?ABCD折叠，使点D，C分别落在点F，E处，（点F，E都在AB所在的直线上），折痕为MN，则∠AMF等于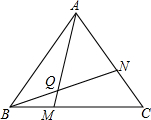
老师布置了一道思考题：
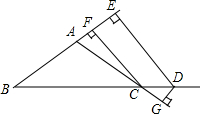如图，已知AB=AC，DE⊥BA的延长线于E，DG⊥AC的延长线于点G，CF⊥BC于点F，试探索DE和CF+DG的关系．
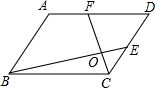如图，平行四边形ABCD中，F为AD中点，CO=
已知AB∥CD，那么∠B+∠BED+∠D等于多少度？为什么？