题目内容
如图，将长方形ABCD沿AE折叠，使D点落在BC边上的点F处，已知AD=10，AB=8，求EC的长．考点：翻折变换（折叠问题）
专题：
分析：如图，根据勾股定理求出BF的长；进而求出FC的长度；由题意得EF=DE；利用勾股定理列出关于EC的方程，解方程即可解决问题．
解答：解：∵四边形ABCD为矩形，
∴DC=AB=8；∠B=∠C=90°；
由题意得：AF=AD=10，EF=DE=λ，EC=8-λ；
由勾股定理得：BF2=102-82，
∴BF=6，CF=10-6=4；
在△EFC中，由勾股定理得：λ2=42+（8-λ）2，
解得：λ=5，EC=8-5=3．
解：∵四边形ABCD为矩形，∴DC=AB=8；∠B=∠C=90°；
由题意得：AF=AD=10，EF=DE=λ，EC=8-λ；
由勾股定理得：BF2=102-82，
∴BF=6，CF=10-6=4；
在△EFC中，由勾股定理得：λ2=42+（8-λ）2，
解得：λ=5，EC=8-5=3．
点评：该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
阅读快车系列答案
相关题目
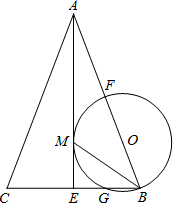如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①b2＞4ac；②abc＞0；③a+b+c=0；④9a+3b+c＜0，其中结论正确的是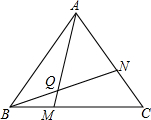
老师布置了一道思考题：
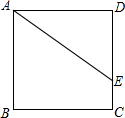如图，正方形ABCD的面积为3，点E是DC边上一点，DE=1，将线段AE绕点A旋转，使点E落在直线BC上，落点记为F，则∠EAF=