题目内容
18.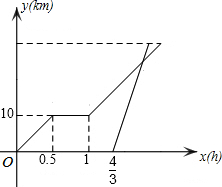 周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在天鹅湖游玩的时间;
(2)求小明从家到天鹅湖和从天鹅湖到巢湖湿地公园路程y(km)与时间x(h)的函数关系式;
(3)小明从家出发多少小时后被妈妈追上?此时离家多远?
(4)如果小明比妈妈晚10分钟到达巢湖湿地公园,请你直接写出他们从天鹅湖到巢湖湿地公园的路程.
分析 (1)根据图象可以求出小明在甲地游玩的时间,由速度=路程÷时间就可以求出小明骑车的速度;
(2)直接运用待定系数法就可以求出从家到天鹅湖和从天鹅湖到巢湖湿地公园路程y(km)与时间x(h)的函数关系式;
(3)其解析式建立二元一次方程组,求出交点的坐标就可以求出结论;
(4)设从妈妈追上小明的地点到巢湖湿地公园的路程为n(km),根据妈妈比小明早到10分钟列出有关n的方程,求得n值即可.
解答 解:(1)由图象得:
在天鹅湖游玩的时间是1-0.5=0.5(h).
小明骑车速度:10÷0.5=20(km/h);
(2)妈妈驾车速度:20×3=60(km/h)
设直线OA的解析式为y=kx(k≠0),
则10=0.5k,
解得:k=20,
故直线OA的解析式为:y=20x.
∵小明走OA段与走BC段速度不变,
∴OA∥BC.
设直线BC解析式为y=20x+b1,
把点B(1,10)代入得b1=-10
∴y=20x-10;
小明从家到天鹅湖和从天鹅湖到巢湖湿地公园路程y(km)与时间x(h)的函数关系式:
从家到天鹅湖的解析式是:y=20x;
从天鹅湖到巢湖湿地公园的解析式为:y=20x-10;
(3)设直线DE解析式为y=60x+b2,把点D($\frac{4}{3}$,0)
代入得:b2=-80
∴y=60x-80;
根据题意可得:$\left\{\begin{array}{l}{y=20x-10}\\{y=60x-80}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1.75}\\{y=25}\end{array}\right.$,
所以小明出发1.75小时(105分钟)被妈妈追上,此时离家25km;
(4)设从妈妈追上小明的地点到巢湖湿地公园的路程为n(km),
由题意得:$\frac{n}{20}-\frac{n}{60}=\frac{10}{60}$,
∴n=5
∴从家到巢湖湿地公园的路程为5+25=30(km).
从天鹅湖到巢湖湿地公园的路程:30-10=20km.
点评 本题考查了一次函数的应用,解题的关键是根据实际问题并结合函数的图象得到进一步解题的有关信息,并从实际问题中整理出一次函数模型.

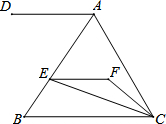 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.(1)求∠FEC的度数;
(2)若∠BAC=3∠B,求证:AB⊥AC;
(3)当∠DAB=50°时,CF⊥AB.
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中九年级人数为408人,下表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中九年级人数为408人,下表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:| 图书种类 | 频数 | 频率 |
| 科普常识 | 840 | B |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | A | 0.25 |
| 其他 | 144 | 0.06 |
(2)求表中A,B的值;A=600,B=0.35.
(3)该校学生平均每人读多少本课外书?
(4)某新华书店新进一种科普常识类课外书籍,其进价是每本6元,这种课外书的月销售量y(本)是每本的销售价x(元)的一次函数,且当x=8时y=120;当x=10时y=100.为答谢广大读者,让利顾客,请计算该新华书店的这种课外书月销售利润为330元时的销售单价.
 甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )
甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )| A. | 甲的速度为60千米/小时 | B. | 乙从A地到B地用了3小时 | ||
| C. | 甲比乙晚出发0.5小时 | D. | 甲到达B地时,乙离A地80千米 |
| A. | a×a=a2n | B. | -(-a)=a | C. | a×a×a=a | D. | a•(-a)=-a |

 汽车油箱中原有汽油若干,如果不再加油,那么油箱中的剩油量y(单位:L)与行驶路程x(单位:km)的寒素关系如图.
汽车油箱中原有汽油若干,如果不再加油,那么油箱中的剩油量y(单位:L)与行驶路程x(单位:km)的寒素关系如图. 如图,已知△ABC
如图,已知△ABC