题目内容
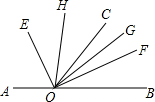 如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数.
如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数.考点:角平分线的定义
专题:
分析:先由OE平分∠AOC,OF平分∠BOC,根据角平分线定义得到∠EOC=
∠AOC,∠COF=
∠BOC,再求出∠EOF=∠EOC+∠COF=
∠AOB=90°;再由OH平分∠COE,OG平分∠COF,根据角平分线定义得到∠HOC=
∠EOC,∠COG=
∠COF,再求出∠GOH=∠HOC+∠COG=
∠EOF=45°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=
∠AOC,∠COF=
∠BOC,
∴∠EOF=∠EOC+∠COF=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB=90°;
∵OH平分∠COE,OG平分∠COF,
∴∠HOC=
∠EOC,∠COG=
∠COF,
∴∠GOH=∠HOC+∠COG=
∠EOC+
∠COF=
(∠EOC+∠COF)=
∠EOF=45°.
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠EOC+∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵OH平分∠COE,OG平分∠COF,
∴∠HOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GOH=∠HOC+∠COG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角平分线定义和角的有关计算的应用,主要考查学生计算能力和推理能力,比较简单.

练习册系列答案
相关题目
 如图,在△ABC中,AD为中线,AE为角平分线,CF⊥AE于点F,AC=4,AB=6,则DF的长为( )
如图,在△ABC中,AD为中线,AE为角平分线,CF⊥AE于点F,AC=4,AB=6,则DF的长为( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
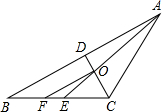 如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )
如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )A、∠OAB=
| ||
| B、∠OEC=∠OCE | ||
C、∠OAB=
| ||
| D、OC⊥OF | ||
| E、∠OEC=∠OCE |
若多边形的边数由3开始增加,则其外角和( )
| A、增加 | B、不变 |
| C、减少 | D、(n-2)×180° |
 如图,在△ABC中,∠B=∠C,AD为BC上的中线,DE⊥AB于点E,DF⊥AC于点F,求证:DA平分∠EDF.
如图,在△ABC中,∠B=∠C,AD为BC上的中线,DE⊥AB于点E,DF⊥AC于点F,求证:DA平分∠EDF.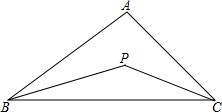 如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y 已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.
已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.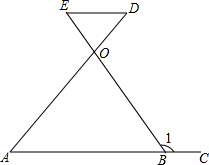 已知,∠1=130°,∠D=50°,∠ABE=∠A,证明:AB∥DE.
已知,∠1=130°,∠D=50°,∠ABE=∠A,证明:AB∥DE.