题目内容
(1)通过计算(可用计算器),比较下列各对数的大小,并提出你的猜想:
①sin30° 2sin15°cos15°;
②sin36° 2sin18°cos18°;
③sin45° 2sin22.5°cos22.5°;
④sin60° 2sin30°cos30°;
⑤sin80° 2sin40°cos40°.
猜想:已知0°<α<45°,则sin2α 2sinαcosα.
(2)如图,在△ABC中,AB=AC=1,∠BAC=2α,请根据提示,利用面积方法验证结论.

①sin30°
②sin36°
③sin45°
④sin60°
⑤sin80°
猜想:已知0°<α<45°,则sin2α
(2)如图,在△ABC中,AB=AC=1,∠BAC=2α,请根据提示,利用面积方法验证结论.

考点:计算器—三角函数
专题:
分析:(1)根据计算器的使用,可得2倍角三角函数;
(2)根据同一个三角形面积的不同表示,可得答案.
(2)根据同一个三角形面积的不同表示,可得答案.
解答:解:(1)通过计算(可用计算器),比较下列各对数的大小,并提出你的猜想:
①sin30°=2sin15°cos15°;
②sin36°=2sin18°cos18°;
③sin45°=2sin22.5°cos22.5°;
④sin60°=2sin30°cos30°;
⑤sin80°=2sin40°cos40°.
(2)已知0°<α<45°,则sin2α=2sinαcosα,
证明:S△ABC=
AB•sing2α•AC,S△ABC=
×2ABsinα•ACcosα,
∴sin2α=2sinαcosα.
①sin30°=2sin15°cos15°;
②sin36°=2sin18°cos18°;
③sin45°=2sin22.5°cos22.5°;
④sin60°=2sin30°cos30°;
⑤sin80°=2sin40°cos40°.
(2)已知0°<α<45°,则sin2α=2sinαcosα,
证明:S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴sin2α=2sinαcosα.
点评:本题考查了计算器-三角函数,利用计算器得出三角函数值,又利用了三角形的面积公式.

练习册系列答案
相关题目
如图是一个几何体的三视图,则该几何体的体积为( )

| A、6 | B、8 | C、16 | D、24 |
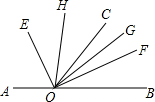 如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数.
如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数. 如图,等边△OAB的一边OA在x轴上,双曲线y=
如图,等边△OAB的一边OA在x轴上,双曲线y= 在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.
在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.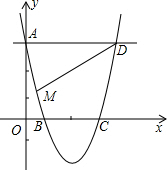 如图,已知点D(4,3)及经过A(0,3),B(1,0),C(3,0)三点的抛物线.
如图,已知点D(4,3)及经过A(0,3),B(1,0),C(3,0)三点的抛物线.