题目内容
11.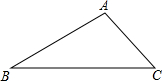 已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
分析 先根据三角形内角和定理求出∠C的度数,再过点A作AD⊥BC于点D,根据锐角三角函数的定义求出AD的长,再根据勾股定理求出BD的长,进而可得出结论.
解答  解:∵∠A=105°,∠B=30°.
解:∵∠A=105°,∠B=30°.
∴∠C=45°.
过点A作AD⊥BC于点D,
∴∠ADB=∠ADC=90°
在Rt△ADC中,
∵∠ADC=90°,∠C=45°,AC=2.
∴∠DAC═∠C=45°.
∵sinC=$\frac{AD}{AC}$,
∴AD=$\sqrt{2}$.
∴AD=CD=$\sqrt{2}$.
在Rt△ADB中,∠ADB=90°,∠B=30°.
∵AD=$\sqrt{2}$,
∴AB=2$\sqrt{2}$.
∴由勾股定理得:BD=$\sqrt{A{B^2}-A{D^2}}=\sqrt{6}$.
∴BC=BD+CD=$\sqrt{6}+\sqrt{2}$.
点评 本题考查的是解直角三角形及勾股定理、锐角三角函数的定义等知识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
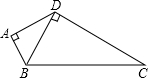 如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2.
如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2.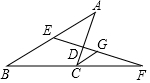 如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长.
如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长.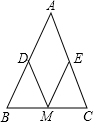 如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.
如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点. 如图,一次函数y1=ax+b的图象与反比例 函数y2=$\frac{k}{x}$的图象交于M,N两点.
如图,一次函数y1=ax+b的图象与反比例 函数y2=$\frac{k}{x}$的图象交于M,N两点.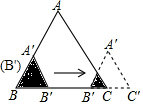 如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )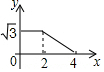
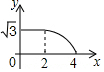
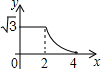
 如图,在钝角三角形ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是2.5秒或4秒.
如图,在钝角三角形ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是2.5秒或4秒.