题目内容
1. 如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2.
如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2.
分析 过D作DE⊥BC于E,根据三角形内角和定理求出∠ABD=∠DBC,根据角平分线性质得出即可.
解答 解:
过D作DE⊥BC于E,则点D到BC边的距离是DE的长度,
∵∠A=90°,∠BDC=90°,∠ADB=∠C,∠A+∠ADB+∠ABD=180°,∠DBC+∠C+∠BDC=180°,
∴∠ABD=∠DBC,
∵∠A=90°,DE⊥BC,AD=2,
∴AD=DE=2,
故答案为:2.
点评 本题考查了三角形内角和定理,角平分线性质的应用,能根据角平分线性质进行推理是解此题的关键.

练习册系列答案
相关题目
3.下列说法中正确的是( )
| A. | 正整数与正分数统称为正有理数 | B. | 正整数与负整数统称为整数 | ||
| C. | 正分数、0、负分数统称为分数 | D. | 一个有理数不是正数就是负数 |
 如图,一张长方形纸片ABCD沿EF折叠,若∠DEF=110°,∠DEA=40度.
如图,一张长方形纸片ABCD沿EF折叠,若∠DEF=110°,∠DEA=40度.
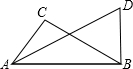 如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长.
如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长. 如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( ) 已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.