题目内容
1. 如图,在钝角三角形ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是2.5秒或4秒.
如图,在钝角三角形ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是2.5秒或4秒.
分析 根据相似三角形的性质,由题意可知有两种相似形式,△ADE∽△ABC和△ADE∽△ACB,可求运动的时间是3秒或4.8秒.
解答 解:根据题意得:设当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是x秒,
①若△ADE∽△ABC,
则$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∴$\frac{x}{5}$=$\frac{10-2x}{10}$,
解得:x=2.5;
②若△ADE∽△ACB,则$\frac{AD}{AC}$=$\frac{AE}{AB}$,
∴$\frac{x}{10}$=$\frac{10-2x}{5}$,
解得:x=4.
∴当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是2.5秒或4秒.
故答案为:2.5秒或4秒.
点评 此题考查了相似三角形的性质,解题时要注意此题有两种相似形式,别漏解;还要注意运用方程思想解题.

练习册系列答案
相关题目
9. 已知函数y=$\frac{4}{|x|}$,小明研究该函数的图象及性质时,列出y与x的几组对应值如下表:
已知函数y=$\frac{4}{|x|}$,小明研究该函数的图象及性质时,列出y与x的几组对应值如下表:
请解答下列问题:
(1)根据表格中给出的数值,在平面直角坐标系xOy中,指出以各对对应值为坐标的点,并画出该函数的图象;
(2)写出该函数的两条性质:①图象关于y轴对称;②图象在x轴的上方.
 已知函数y=$\frac{4}{|x|}$,小明研究该函数的图象及性质时,列出y与x的几组对应值如下表:
已知函数y=$\frac{4}{|x|}$,小明研究该函数的图象及性质时,列出y与x的几组对应值如下表:请解答下列问题:
| x | … | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | … |
| y | … | 1 | $\frac{4}{3}$ | 2 | 4 | 4 | 2 | $\frac{4}{3}$ | 1 |
(2)写出该函数的两条性质:①图象关于y轴对称;②图象在x轴的上方.
16.在解方程$\frac{1-2x}{3}$=1-$\frac{3x+1}{6}$时要先去分母,则下列去分母中正确的是( )
| A. | 2-4x=1-3x+1 | B. | 2(1-2x)=1-(3x+1) | C. | 2-4x=6-3x+1 | D. | 2(1-2x)=6-(3x+1) |
6. 如图,直线a∥b,∠1=125°,则∠2的度数为( )
如图,直线a∥b,∠1=125°,则∠2的度数为( )
 如图,直线a∥b,∠1=125°,则∠2的度数为( )
如图,直线a∥b,∠1=125°,则∠2的度数为( )| A. | 75° | B. | 65° | C. | 55° | D. | 45° |
10.某人在A处看点B在北偏东40°的方向上,看点C在北偏东35°的方向上,则∠BAC的度数为( )
| A. | 45° | B. | 5° | C. | 40° | D. | 35° |
 已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.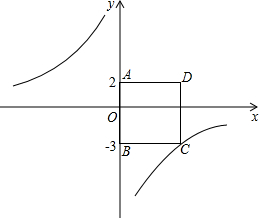 如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=$\frac{k}{x}$的图象经过点C.
如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=$\frac{k}{x}$的图象经过点C.