题目内容
6.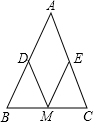 如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.
如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.(1)求证:MD=ME;
(2)若MD=5,求AC的长.
分析 (1)连结AM,根据等腰三角形三线合一的性质得到AM⊥BC,再根据直角三角形斜边上的中线等于斜边的一半得出MD=$\frac{1}{2}$AB,ME=$\frac{1}{2}$AC,进而得到MD=ME;
(2)根据(1)可得AB=2MD=10,那么AC=AB=10.
解答 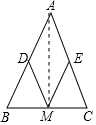 (1)证明:如图,连结AM.
(1)证明:如图,连结AM.
∵AB=AC,M是BC的中点,
∴AM⊥BC,
∵D、E分别是AB、AC的中点,
∴MD=$\frac{1}{2}$AB,ME=$\frac{1}{2}$AC,
∵AB=AC,
∴MD=ME;
(2)解:∵MD=$\frac{1}{2}$AB,
∴AB=2MD=10,
∴AC=AB=10.
点评 本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半,也考查了等腰三角形三线合一的性质.

练习册系列答案
相关题目
16.在解方程$\frac{1-2x}{3}$=1-$\frac{3x+1}{6}$时要先去分母,则下列去分母中正确的是( )
| A. | 2-4x=1-3x+1 | B. | 2(1-2x)=1-(3x+1) | C. | 2-4x=6-3x+1 | D. | 2(1-2x)=6-(3x+1) |
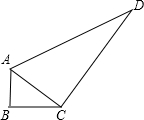 一块钢板形状如图所示,量得AB=3,BC=4,AC=5,CD=12,AD=13,请你计算一下这块钢板的面积.
一块钢板形状如图所示,量得AB=3,BC=4,AC=5,CD=12,AD=13,请你计算一下这块钢板的面积. 已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.