题目内容
16. 如图,一次函数y1=ax+b的图象与反比例 函数y2=$\frac{k}{x}$的图象交于M,N两点.
如图,一次函数y1=ax+b的图象与反比例 函数y2=$\frac{k}{x}$的图象交于M,N两点.(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)观察图象,比较y1与y2的大小.
分析 (1)根据点N的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数解析式,由点M的横坐标结合反比例函数图象上点的坐标特征即可得出点M的坐标,再根据点M、N的坐标利用待定系数法即可求出一次函数解析式,此题得解;
(2)观察图形,根据两函数图象的上下位置关系即可得出结论.
解答 解:(1)∵反比例函数y2=$\frac{k}{x}$的图象过点N(-1,-4),
∴k=-1×(-4)=4,
∴反比例函数的解析式为y2=$\frac{4}{x}$.
∵点M(2,m)在反比例函数y2=$\frac{4}{x}$的图象上,
∴m=$\frac{4}{2}$=2,
∴点M的坐标为(2,2).
将M(2,2)、N(-1,-4)代入y1=ax+b中,
$\left\{\begin{array}{l}{2a+b=2}\\{-a+b=-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=-2}\end{array}\right.$,
∴一次函数的解析式为y=2x-2.
(2)观察函数图象,由两函数图象的上下位置关系可知:
当x<-1或0<x<2时,y1<y2;当x=-1或x=2时,y1=y2;当-1<x<0或x>2时,y1>y2.
点评 本题考查了反比例函数图象上点的坐标特征、待定系数法求一次函数解析式以及反比例函数与一次函数的交点问题,根据点的坐标利用待定系数法求出函数解析式是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
4.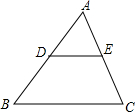 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
1.(1.2计算3.4分解因式)
(1)($\sqrt{2}$+1)0-(-$\frac{1}{2}$)2+2-2
(2)(2a-3b)(-3b-2a)
(3)3m2-24m+48
(4)x3y-4xy.
(1)($\sqrt{2}$+1)0-(-$\frac{1}{2}$)2+2-2
(2)(2a-3b)(-3b-2a)
(3)3m2-24m+48
(4)x3y-4xy.
6. 如图,直线a∥b,∠1=125°,则∠2的度数为( )
如图,直线a∥b,∠1=125°,则∠2的度数为( )
 如图,直线a∥b,∠1=125°,则∠2的度数为( )
如图,直线a∥b,∠1=125°,则∠2的度数为( )| A. | 75° | B. | 65° | C. | 55° | D. | 45° |
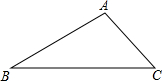 已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长.
已知:如图,在△ABC中,∠A=105°,∠B=30°,AC=2.求BC的长. 如图,AB与DE相交于点O,OC⊥AB,OF是∠AOE的角平分线,若∠COD=36°,则∠AOF=27°.
如图,AB与DE相交于点O,OC⊥AB,OF是∠AOE的角平分线,若∠COD=36°,则∠AOF=27°.