Question

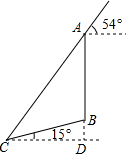如图，在一个坡角为15°的斜坡上有一棵树，高为AB，当太阳光线与水平线成54°角时，测得该树斜坡上的树影BC的长为10m，延长AB，交过点C的水平线于点D，求BD与树高AB（精确到0.1m），（已知sin15°≈0.259，cos15°≈0.966，tan15°≈0.268，sin54°≈0.809，cos54°≈0.588，tan54°≈1.376．供选用）．

Answer 1

考点：解直角三角形的应用-坡度坡角问题

专题：

分析：过C作AB的垂线，设垂足为D．在Rt△CDB中，已知斜边BC=10m，利用三角函数求出CD和BD的长．同理在△ACD中，已知∠ACD=52°，CD，求出AD长，计算出AB=AD-BD，从而得到树的高度．

解答：解：作CD⊥AB于D．
在Rt△BCD中，BC=10m，∠BCD=15°，
∴CD=BC•cos15°≈10×0.966=9.66（m），
BD=BC•sin15°≈10×0.259=2.59（m）；
在Rt△ACD中，CD=9.66m，∠ACD=54°，
∴AD=CD•tan54°≈9.66×1.376=13.292（m）．
∴AB=AD-BD=13.292-2.59≈10.7（m）．
答：树高10.7米．

点评：本题考查了解直角三角形中有关坡角问题：把问题转化为解直角三角形，已知一边和一锐角可解此直角三角形．