题目内容
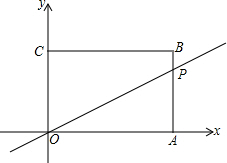 如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t
如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t探究:
(1)当t为何值时,线段OP最长,是多少?
(2)S与t的函数关系?并指出是什么函数关系?
(3)当t为何值时,S=9,此时OP在矩形中扫过的面积是一个什么几何图形?
考点:四边形综合题
专题:
分析:(1)根据图示知,当点P与点B重合时,线段OP最长;
(2)分段函数:点P在线段AB上和点P在线段BC上两段函数.在线段AB上时,S=S△AOP;在线段BC上时,S=S梯形OABP;
(3)把S=9代入(2)中的函数解析式,求得相应的t的值,则推知点P所在的位置,根据点P的位置来推断OP在矩形中扫过的面积是何种几何图形.
(2)分段函数:点P在线段AB上和点P在线段BC上两段函数.在线段AB上时,S=S△AOP;在线段BC上时,S=S梯形OABP;
(3)把S=9代入(2)中的函数解析式,求得相应的t的值,则推知点P所在的位置,根据点P的位置来推断OP在矩形中扫过的面积是何种几何图形.
解答: 解:如图,∵四边形OABC是矩形,A(4,0),C(0,3),
解:如图,∵四边形OABC是矩形,A(4,0),C(0,3),
∴BC∥OA,OC=AB=3,OA=CB=4,∠OAB=∠ABC=90°.
(1)当点P与点B重合时,OP的长度最大.此时t=3.
在Rt△OAP中,利用勾股定理得到:OP=OB=
=
=5,
综上所述,当t=3时,线段OP最长,为5;
(2)分两种情况:
①当点P在线段AB上时,S=
OA•AP=
×4×t=2t(0<t≤3),该函数是正比例函数;
②当点P在线段BC上时,S=S梯形OABP=
×3=
t+
(3<t≤7),该函数是一次函数.
综上所述,
S=
;
(3)∵由(2)知,当点P在线段AB上时,S=2t(0<t≤3),则S最大=2×3=6.
∴当S=9时,点P在线段BC上.
∴9=
t+
,
解得 t=5,
∴点P不与点C重合,即OP与AB不平行,且OP≠AB
又∵BC∥OA,∠OAB=∠ABP=90°.
∴四边形OABP是直角梯形.
 解:如图,∵四边形OABC是矩形,A(4,0),C(0,3),
解:如图,∵四边形OABC是矩形,A(4,0),C(0,3),∴BC∥OA,OC=AB=3,OA=CB=4,∠OAB=∠ABC=90°.
(1)当点P与点B重合时,OP的长度最大.此时t=3.
在Rt△OAP中,利用勾股定理得到:OP=OB=
| OA2+AB2 |
| 42+32 |
综上所述,当t=3时,线段OP最长,为5;
(2)分两种情况:
①当点P在线段AB上时,S=
| 1 |
| 2 |
| 1 |
| 2 |
②当点P在线段BC上时,S=S梯形OABP=
| t-3+4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
综上所述,
S=
|
(3)∵由(2)知,当点P在线段AB上时,S=2t(0<t≤3),则S最大=2×3=6.
∴当S=9时,点P在线段BC上.
∴9=
| 3 |
| 2 |
| 3 |
| 2 |
解得 t=5,
∴点P不与点C重合,即OP与AB不平行,且OP≠AB
又∵BC∥OA,∠OAB=∠ABP=90°.
∴四边形OABP是直角梯形.
点评:本题考查了四边形综合题.涉及到了三角形的面积、梯形的面积的求法,矩形的性质,列函数关系式以及直角梯形的判定方法.注意:在(3)中,推知四边形OABP是直角梯形的过程中,必须先推知OP与AB不平行,且OP≠AB,以排除四边形OABP是矩形和等腰梯形的情况.

练习册系列答案
相关题目
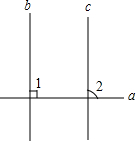 如图,已知直线b∥c,a⊥b,求证:a⊥c.
如图,已知直线b∥c,a⊥b,求证:a⊥c.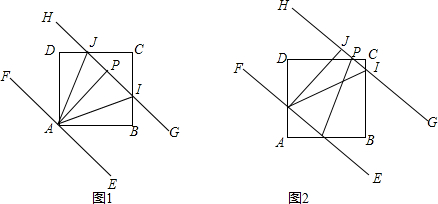
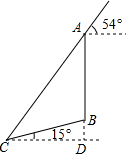 如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).
如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).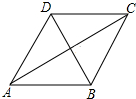 如图,有一张菱形纸片ABCD,AC=8,BD=6.
如图,有一张菱形纸片ABCD,AC=8,BD=6.