题目内容
 如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).
如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx-k的值大于函数y=x的值的自变量x的取值范围.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)先把A(m,2)代入正比例函数解析式可计算出m=2,然后把A(2,2)代入y=kx-k计算出k的值,从而得到一次函数解析式为y=2x-2;
(2)先确定B点坐标,然后根据三角形面积公式计算;
(3)观察函数图象得到当x>2时,直线y=kx-k都在y=x的上方,即函数y=kx-k的值大于函数y=x的值.
(2)先确定B点坐标,然后根据三角形面积公式计算;
(3)观察函数图象得到当x>2时,直线y=kx-k都在y=x的上方,即函数y=kx-k的值大于函数y=x的值.
解答:解:(1)把A(m,2)代入y=x得m=2,则点A的坐标为(2,2),
把A(2,2)代入y=kx-k得2k-k=2,解得k=2,
所以一次函数解析式为y=2x-2;
(2)把x=0代入y=2x-2得y=-2,则B点坐标为(0,-2),
所以S△AOB=
×2×2=2;
(3)自变量x的取值范围是x>2.
把A(2,2)代入y=kx-k得2k-k=2,解得k=2,
所以一次函数解析式为y=2x-2;
(2)把x=0代入y=2x-2得y=-2,则B点坐标为(0,-2),
所以S△AOB=
| 1 |
| 2 |
(3)自变量x的取值范围是x>2.
点评:本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
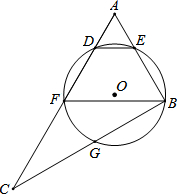 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+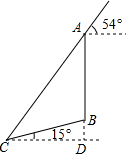 如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).
如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).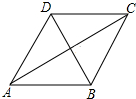 如图,有一张菱形纸片ABCD,AC=8,BD=6.
如图,有一张菱形纸片ABCD,AC=8,BD=6.