题目内容
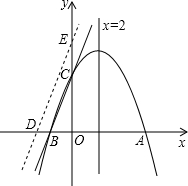 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).(1)求点B的坐标;
(2)已知a=-1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=3S△BOC,求点P的坐标;
②当直线BC左右平移时,直线与x轴、y轴分别交于D、E,对称轴上是否存在点M,使得△DEM为等腰直角三角形?若存在,直接写出点M的坐标;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)由抛物线y=ax2+bx+c的对称轴为直线x=2,交x轴于A、B两点,其中A点的坐标为(5,0),根据二次函数的对称性,即可求得B点的坐标;
(2)①a=-1时,先由对称轴为直线x=2,求出b的值,再将B(-1,0)代入,求出二次函数的解析式为y=-x2+2x+3,得到C点坐标,然后设P点坐标为(x,-x2+2x+3),根据S△POC=3S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
②当∠PDE=90°时,先运用待定系数法求出直线BC的解析式为y=3x+3,再设则直线DE为:y=3x+3+b,求得D(-
,0),E(0,3+b),得出DG=2+
,OE=3+b,然后根据△DOE≌△MGD得出DG=OE,进而求得GM的长,即可求得M的坐标;当∠DME=90°时,根据题意△EFM≌△NMD,得出MN=EF=2,即可求得M的坐标.
(2)①a=-1时,先由对称轴为直线x=2,求出b的值,再将B(-1,0)代入,求出二次函数的解析式为y=-x2+2x+3,得到C点坐标,然后设P点坐标为(x,-x2+2x+3),根据S△POC=3S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
②当∠PDE=90°时,先运用待定系数法求出直线BC的解析式为y=3x+3,再设则直线DE为:y=3x+3+b,求得D(-
| 3+b |
| 3 |
| 3+b |
| 3 |
解答:解:(1)∵对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,
∴A、B两点关于直线x=2对称,
∵点A的坐标为(5,0),
∴点B的坐标为(-1,0);
(2)①a=-1时,∵抛物线y=-x2+bx+c的对称轴为直线x=2,
∴
=2,解得b=4.
将B(-1,0)代入y=-x2+4x+c,
得-1-4+c=0,解得c=5.
则二次函数的解析式为y=-x2+4x+5,
∴抛物线与y轴的交点C的坐标为(0,5),OC=5.
设P点坐标为(x,-x2+4x+5),
∵S△POC=4S△BOC,
∴
×5×|x|=3×
×5×1,
∴|x|=3,x=±
.
当x=
时,-x2+2x+3=2
当x=-
时,-x2+2x+3=-2
∴点P的坐标为(
,2
)或(-
,-2
);
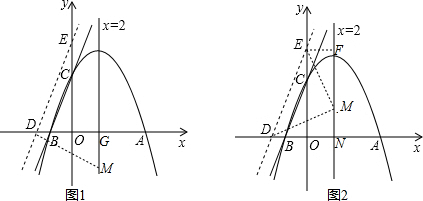
②有两种情况:
当∠PDE=90°时,∵点B的坐标为(-1,0),C(0,3),
∴直线BC为:y=3x+3,
∴直线DE为:y=3x+3+b,
∴D(-
,0),E(0,3+b),
∴DG=2+
,OE=3+b,
∵△DEM为等腰直角三角形,
∴△DOE≌△MGD,
∴DG=OE,
∴2+
=3+b,
解得:b=0,
∴MG=OB=1,
∴M(2,-1),
当∠DME=90°时,根据题意△EFM≌△NMD,
∴MN=EF=2,
∴M(2,2).
∴A、B两点关于直线x=2对称,
∵点A的坐标为(5,0),
∴点B的坐标为(-1,0);
(2)①a=-1时,∵抛物线y=-x2+bx+c的对称轴为直线x=2,
∴
| -b |
| -1×2 |
将B(-1,0)代入y=-x2+4x+c,
得-1-4+c=0,解得c=5.
则二次函数的解析式为y=-x2+4x+5,
∴抛物线与y轴的交点C的坐标为(0,5),OC=5.
设P点坐标为(x,-x2+4x+5),
∵S△POC=4S△BOC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴|x|=3,x=±
| 3 |
当x=
| 3 |
| 3 |
当x=-
| 3 |
| 3 |
∴点P的坐标为(
| 3 |
| 3 |
| 3 |
| 3 |
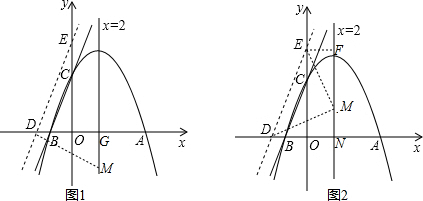
②有两种情况:
当∠PDE=90°时,∵点B的坐标为(-1,0),C(0,3),
∴直线BC为:y=3x+3,
∴直线DE为:y=3x+3+b,
∴D(-
| 3+b |
| 3 |
∴DG=2+
| 3+b |
| 3 |
∵△DEM为等腰直角三角形,
∴△DOE≌△MGD,
∴DG=OE,
∴2+
| 3+b |
| 3 |
解得:b=0,
∴MG=OB=1,
∴M(2,-1),
当∠DME=90°时,根据题意△EFM≌△NMD,
∴MN=EF=2,
∴M(2,2).
点评:此题考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以及三角形面积、线段长度问题.此题难度适中,解题的关键是运用方程思想与数形结合思想.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、a一定是正数 | ||
| B、没有绝对值最小的实数 | ||
C、2
| ||
D、
|
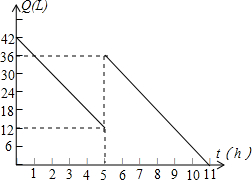 机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.
机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图回答问题.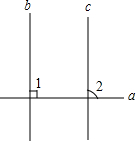 如图,已知直线b∥c,a⊥b,求证:a⊥c.
如图,已知直线b∥c,a⊥b,求证:a⊥c.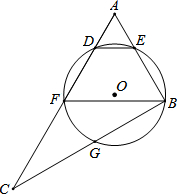 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+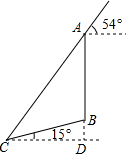 如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).
如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).