题目内容
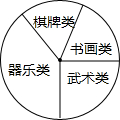 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:
某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:(1)确定调查方式时,甲同学说“我到七(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请你指出哪位同学的调查方式最合理;
(2)他们采用了最合理的调查方法收集数据,并绘制了如图的统计表和如图扇形统计图.
| 类别 | 频数(人数) | 频率 |
| 武术类 | 25 | 0.25 |
| 书画类 | a | 0.20 |
| 棋牌类 | 15 | b |
| 器乐类 | 40 | 0.40 |
| 合计 | 1.00 |
①a=
②在扇形统计图中器乐类所对应扇形的圆心角是
③若该校七年级有学生460人,请你估计大约有多少学生参加书画类校本课程.
考点:频数(率)分布表,用样本估计总体,扇形统计图
专题:
分析:(1)采用随机调查的方式比较合理,随机调查的关键是调查的随机性,这样才合理;
(2)①用喜欢书画类的频数除以喜欢书画类的频率即可求得a值,用喜欢棋牌类的人数除以总人数即可求得b值.
②求得器乐类的频率乘以360°即可.
③用总人数乘以喜欢武术类的频率即可求喜欢武术的总人数.
(2)①用喜欢书画类的频数除以喜欢书画类的频率即可求得a值,用喜欢棋牌类的人数除以总人数即可求得b值.
②求得器乐类的频率乘以360°即可.
③用总人数乘以喜欢武术类的频率即可求喜欢武术的总人数.
解答:解:(1)∵调查的人数较多,范围较大,
∴应当采用随机抽样调查,
∵到六年级每个班随机调查一定数量的同学相对比较全面,
∴丙同学的说法最合理.
(2)①∵喜欢武术类的有25人,百分比为25%,
∴总人数=25÷0.25=100,喜欢书画类的有100-25-15-40=20人,
棋牌类的百分比为15÷100=0.15.
故答案是:20,0.15;
②∵喜欢器乐类的频率为:1-0.25-0.20-0.15=0.4,
∴喜欢器乐类所对应的扇形的圆心角的度数为:360×0.4=144°,
故答案是:144;
③喜欢武术类的人数为:460×0.25=125(人).
∴应当采用随机抽样调查,
∵到六年级每个班随机调查一定数量的同学相对比较全面,
∴丙同学的说法最合理.
(2)①∵喜欢武术类的有25人,百分比为25%,
∴总人数=25÷0.25=100,喜欢书画类的有100-25-15-40=20人,
棋牌类的百分比为15÷100=0.15.
故答案是:20,0.15;
②∵喜欢器乐类的频率为:1-0.25-0.20-0.15=0.4,
∴喜欢器乐类所对应的扇形的圆心角的度数为:360×0.4=144°,
故答案是:144;
③喜欢武术类的人数为:460×0.25=125(人).
点评:本题考查的用样本估计总体和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
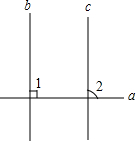 如图,已知直线b∥c,a⊥b,求证:a⊥c.
如图,已知直线b∥c,a⊥b,求证:a⊥c.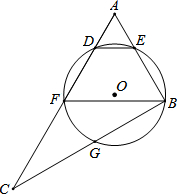 如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+
如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+ 已知实数a、b、c在数轴上对应点的位置如图,化简
已知实数a、b、c在数轴上对应点的位置如图,化简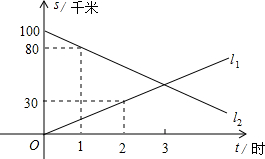 甲、乙两人骑车分别从A、B两地同时出发,相向而行,假设他们都保持匀速行驶,则甲、乙两人各自距A地的距离s(千米)与行驶的时间t(时)的关系分别用图中直线l1、l2在第一象限的部分表示.
甲、乙两人骑车分别从A、B两地同时出发,相向而行,假设他们都保持匀速行驶,则甲、乙两人各自距A地的距离s(千米)与行驶的时间t(时)的关系分别用图中直线l1、l2在第一象限的部分表示.
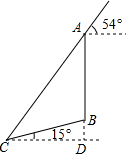 如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).
如图,在一个坡角为15°的斜坡上有一棵树,高为AB,当太阳光线与水平线成54°角时,测得该树斜坡上的树影BC的长为10m,延长AB,交过点C的水平线于点D,求BD与树高AB(精确到0.1m),(已知sin15°≈0.259,cos15°≈0.966,tan15°≈0.268,sin54°≈0.809,cos54°≈0.588,tan54°≈1.376.供选用).