题目内容
如图，在△ABC中，∠ACB=90°，D是AB的中点，DE∥BC交AC于E．如果AC=6，BC=8，那么DE=考点：三角形中位线定理,直角三角形斜边上的中线
专题：
分析：首先利用勾股定理求得AB的长，易证DE是△ABC的中位线，然后依据三角形的中位线定理以及直角三角形斜边上的中线等于斜边的一半即可求解．
解答：解：在直角△ABC中，AB=
=
=10，
∵D是AB的中点，DE∥BC交AC于E，
∴DE是△ABC的中位线，D是AB的中点．
∴DE=
BC=4，CD=
AB=5．
故答案是：4，5．
| AC2+BC2 |
| 62+82 |
∵D是AB的中点，DE∥BC交AC于E，
∴DE是△ABC的中位线，D是AB的中点．
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案是：4，5．
点评：本题考查了勾股定理、三角形的中位线定理以及直角三角形的性质，正确证明DE是中位线是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
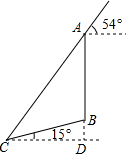如图，在一个坡角为15°的斜坡上有一棵树，高为AB，当太阳光线与水平线成54°角时，测得该树斜坡上的树影BC的长为10m，延长AB，交过点C的水平线于点D，求BD与树高AB（精确到0.1m），（已知sin15°≈0.259，cos15°≈0.966，tan15°≈0.268，sin54°≈0.809，cos54°≈0.588，tan54°≈1.376．供选用）．
如图，在△ABC中，∠C=90°，sinA=
如图，∠DCA=∠ECB，CD=CA，若使△ABC≌△DEC，则下列添加的条件错误的是（ ）| A、CB=CE |
| B、∠B=∠E |
| C、∠A=∠D |
| D、AB=DE |