题目内容
3.下列分式$\frac{{12{b^2}c}}{4a}、\frac{{5(x+y{)^2}}}{y+x}、\frac{{{a^2}+{b^2}}}{3(a+b)}、\frac{{4{a^2}-{b^2}}}{2a-b}、\frac{a-b}{b-a}$中,最简分式的有1个.分析 最简分式的标准是分子、分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:$\frac{12{b}^{2}c}{4a}$=$\frac{3{b}^{2}c}{a}$,
$\frac{5(x+y)^{2}}{y+x}$=5(x+y),
$\frac{{a}^{2}+{b}^{2}}{3(a+b)}$是最简分式,
$\frac{4{a}^{2}-{b}^{2}}{2a-b}$=2a+b,
$\frac{a-b}{b-a}$=-1,
则最简分式的有1个;
故答案为:1.
点评 本题考查了最简分式,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
16.在平面直角坐标系xOy中,若将直线y=ax+2先沿y轴方向向上平移3个单位,再沿x轴方向向右平移2个单位,最后得到的直线与原直线重合,则实数a的值是( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
18. 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,
l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为
( )
 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为
( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
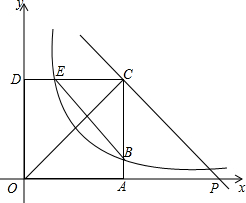 如图所示,点A坐标为(4,0),矩形OACD的两边AC与CD分别交双曲线y=$\frac{4}{x}$(x>0)于B,E两点,记$\frac{BC}{AB}$=k,过点C作CP∥BE交x轴于点P.
如图所示,点A坐标为(4,0),矩形OACD的两边AC与CD分别交双曲线y=$\frac{4}{x}$(x>0)于B,E两点,记$\frac{BC}{AB}$=k,过点C作CP∥BE交x轴于点P.


