题目内容
11.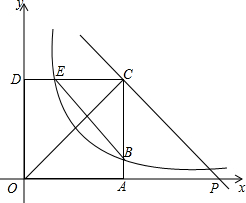 如图所示,点A坐标为(4,0),矩形OACD的两边AC与CD分别交双曲线y=$\frac{4}{x}$(x>0)于B,E两点,记$\frac{BC}{AB}$=k,过点C作CP∥BE交x轴于点P.
如图所示,点A坐标为(4,0),矩形OACD的两边AC与CD分别交双曲线y=$\frac{4}{x}$(x>0)于B,E两点,记$\frac{BC}{AB}$=k,过点C作CP∥BE交x轴于点P.(1)当k=1时,点B坐标为(4,1),点E坐标为(2,2),点P坐标为(8,0).
(2)当k=2时,点B坐标为(4,1),点E坐标为($\frac{4}{3}$,3),点P坐标为(8,0).
(3)当k值变化时,判断点P的坐标是否发生变化,并说明理由.
分析 (1)根据点A的坐标以及矩形的性质可得出点B的坐标,结合k的值即可得出点C的坐标以及点E的坐标,再根据线段CE、DE之间的关系利用平行线的判定定理找出BE∥AD,即可得出CP∥AD,进而可得出四边形APCD为平行四边形,根据平行四边形的性质结合点A的坐标即可得出点P的坐标,此题得解;
(2)根据点A的坐标以及矩形的性质可得出点B的坐标,结合k的值即可得出点C的坐标以及点E的坐标,再根据线段CE、DE之间的关系利用平行线的判定定理找出BE∥AD,即可得出CP∥AD,进而可得出四边形APCD为平行四边形,根据平行四边形的性质结合点A的坐标即可得出点P的坐标,此题得解;
(3)连接AD,根据k的值可得出点C的坐标以及点E的坐标,再根据线段CE、DE之间的关系利用平行线的判定定理找出BE∥AD,即可得出CP∥AD,进而可得出四边形APCD为平行四边形,由此即可得出点P的坐标为定值.
解答 解:(1)∵点A坐标为(4,0),四边形OACD为矩形,
∴点B的横坐标为4,
∵点B在交双曲线y=$\frac{4}{x}$(x>0)上,
∴点B的坐标为(4,1).
∵$\frac{BC}{AB}$=k=1,
∴点C的坐标为(4,2),点E的坐标为(2,2),
∴CE=2,DE=2.
连接AD,则$\frac{CE}{DE}$=1,
∴BE∥AD,
∵CP∥BE,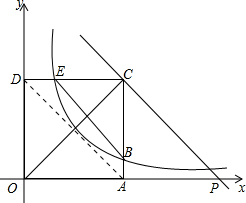
∴CP∥AD,
∵CD∥AP,
∴四边形APCD为平行四边形,
∴AP=CD=OA=4,
∴点P的坐标为(8,0)
故答案为:(4,1);(2,2);(8,0).
(2)∵点A坐标为(4,0),四边形OACD为矩形,
∴点B的横坐标为4,
∵点B在交双曲线y=$\frac{4}{x}$(x>0)上,
∴点B的坐标为(4,1).
∵$\frac{BC}{AB}$=k=2,
∴点C的坐标为(4,3),点E的坐标为($\frac{4}{3}$,3),
∴CE=$\frac{8}{3}$,DE=$\frac{4}{3}$.
连接AD,则$\frac{CE}{DE}$=2,
∴BE∥AD,
∵CP∥BE,
∴CP∥AD,
∵CD∥AP,
∴四边形APCD为平行四边形,
∴AP=CD=OA=4,
∴点P的坐标为(8,0)
故答案为:(4,1);($\frac{4}{3}$,3);(8,0).
(3)点P的坐标不变,理由如下:
连接AD,当$\frac{BC}{AB}$=k时,B(4,1),
∴AC=k+1,
∴点E的坐标为($\frac{4}{k+1}$,k+1),
∴DE=$\frac{4}{k+1}$,EC=4-$\frac{4}{k+1}$=$\frac{4k}{k+1}$,
∴$\frac{EC}{DE}$=k,
∴BE∥AD.
∵CP∥BE,
∴CP∥AD,
∵CD∥AP,
∴四边形APCD为平行四边形,
∴AP=CD=OA=4,
∴点P的坐标为(8,0).
点评 本题考查了反比例函数图象上点的坐标特征、平行线的判定与性质以及平行四边形的判定与性质,解题的关键是找出四边形APCD为平行四边形.

| A. | 所有的有理数都能用数轴上的点表示 | |
| B. | 有理数分为正数及负数 | |
| C. | 0没有相反数 | |
| D. | 0的倒数仍为0 |
| A. | ($\sqrt{3}$+$\sqrt{7}$)•$\sqrt{10}$=$\sqrt{10}$•$\sqrt{10}$=10 | B. | (6-2$\sqrt{3}$)(6+2$\sqrt{3}$)=36-6=30 | ||
| C. | (a$\sqrt{x}$+b$\sqrt{x}$)(a$\sqrt{x}$-b$\sqrt{x}$)=(a2-b2)x | D. | $\sqrt{6}$+$\sqrt{18}$=2$\sqrt{3}$+2$\sqrt{9}$=2($\sqrt{3}$+$\sqrt{9}$) |
| A. | 2 | B. | 2abc | C. | 2ab2c | D. | 2a2b2c |
 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | (-1,1) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
| A. | 57×103 | B. | 5.7×104 | C. | 5.7×105 | D. | 0.57×105 |
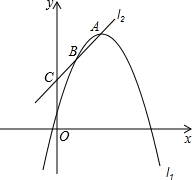 如图,已知,抛物线l1:y=ax2-4ax+5+4a(a<0)的顶点为A,直线l2:y=kx+3过点A,直线l2与抛物线l1及y轴分别交于B,C.
如图,已知,抛物线l1:y=ax2-4ax+5+4a(a<0)的顶点为A,直线l2:y=kx+3过点A,直线l2与抛物线l1及y轴分别交于B,C.