题目内容
3．计算（π-$\sqrt{3}$）0+（$\frac{1}{2}$）-1-|$\sqrt{3}$-1|-tan60°+$\sqrt{12}$．分析 直接化简二次根式、再利用负整数指数幂的性质和特殊角的三角函数值、绝对值的性质分别化简各数得出答案．
解答 解：原式=1+2-（$\sqrt{3}$-1）-$\sqrt{3}$+2$\sqrt{3}$
=4．
点评 此题主要考查了实数运算，正确把握相关性质化简各数是解题关键．
练习册系列答案
相关题目
13．若分式$\frac{2}{x-1}$有意义，则x的取值范围是（ ）
| A． | x=1 | B． | x≠1 | C． | x＞1 | D． | x＜1 |
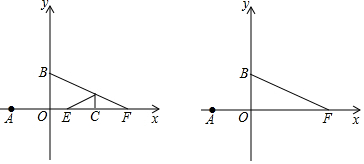
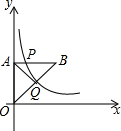如图，平面直角坐标系中，O为坐标原点，等腰Rt△OAB的顶点B在第一象限，直角边OA在y轴上，点P是边AB上的一个三等分点，过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q，△AOQ的面积为3，则k的值为2$\sqrt{3}$或2$\sqrt{6}$．
8．当a=$\sqrt{2}$时，计算分式$\frac{a+3}{a}$•$\frac{6}{{a}^{2}+6a+9}$+$\frac{2a-6}{{a}^{2}-9}$的值是$\sqrt{2}$．
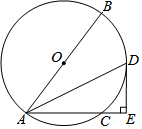如图，AB是⊙O的直径，C点在⊙O上，连接AC，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E．
已知：如图，圆锥的底面直径是10cm，高为12cm，则它的侧面展开图的面积是65πcm2．