题目内容
12.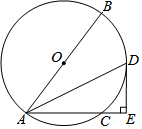 如图,AB是⊙O的直径,C点在⊙O上,连接AC,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
如图,AB是⊙O的直径,C点在⊙O上,连接AC,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.(1)求证:DE是⊙O的切线;
(2)若AB=10,sin∠BAC=$\frac{4}{5}$,连接CD,求CD的长.
分析 (1)连接OD,欲证明DE是⊙O的切线,只要证明OD⊥DE即可.
(2)过点O作OF⊥AC于点F,只要证明四边形OFED是矩形即可得到DE=OF,在RT△AOF中利用勾股定理求出OF,然后根据切割线定理结论得到结论.
解答 (1)证明:连接OD,
∵AD是∠BAC的平分线,
∴∠OAD=∠DAE.
∵OA=OD,
∴∠OAD=∠ODA.
∴∠ODA=∠DA E.
∴OD∥AE.
∵DE⊥AC,
∴DE⊥OD.
∴DE是⊙O的切线;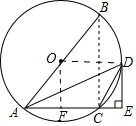
(2)连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=10,sin∠BAC=$\frac{4}{5}$,
∴BC=8,
∴AC=6,
过点O作OF⊥AC于点F,
∴AF=CF=3,
∴OF=$\sqrt{A{O}^{2}-A{F}^{2}}$=4,
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形,
∴DE=OF=4,
∵DE是⊙O的切线,
∴DE2=CE•AE,
∴CE=2,
∴CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=2$\sqrt{5}$.
点评 本题考查切线的判定和性质,矩形的判定和性质、垂径定理、勾股定理等知识,解题的关键是记住切线的判定方法,学会添加常用辅助线,属于基础题,中考常考题型.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
2. 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,
甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,
甲组12户家庭用水量统计表
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,
甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图,甲组12户家庭用水量统计表
| 用水量(吨) | 4 | 5 | 6 | 9 |
| 户数 | 4 | 5 | 2 | 1 |
| A. | 甲组比乙组大 | B. | 甲、乙两组相同 | C. | 乙组比甲组大 | D. | 无法判断 |
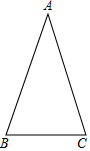 已知等腰△ABC的顶角∠A=36°(如图).
已知等腰△ABC的顶角∠A=36°(如图).