题目内容
2．先化简，再求值：（$\frac{1}{x-1}-1$）$÷\frac{{x}^{2}-4x+4}{x-1}$，其中x=$2+\sqrt{3}$．分析 先算括号里面的，再算除法，把x的值代入进行计算即可．
解答 解：原式=$\frac{1-（x-1）}{x-1}$•$\frac{x-1}{（x-2）^{2}}$
=$\frac{1-x+1}{x-1}$•$\frac{x-1}{{（x-2）}^{2}}$
=$\frac{2-x}{x-1}$•$\frac{x-1}{{（x-2）}^{2}}$
=$\frac{1}{2-x}$，
当x=2+$\sqrt{3}$时，原式=$\frac{1}{2-2-\sqrt{3}}$=-$\frac{\sqrt{3}}{3}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
12．
如图1是手机放在手机支架上，其侧面示意图如图2所示，AB，CD是长度不变的活动片，一端A固定在0A上，另一端B可在0C上变动位置，若将AB变到AB′的位置，则0C旋转一定角度到达0C′的位置．已知0A=8cm，AB⊥0C，∠B0A=60°，sin∠B′A0=$\frac{9}{10}$，则点B′到0A的距离为（ ）
如图1是手机放在手机支架上，其侧面示意图如图2所示，AB，CD是长度不变的活动片，一端A固定在0A上，另一端B可在0C上变动位置，若将AB变到AB′的位置，则0C旋转一定角度到达0C′的位置．已知0A=8cm，AB⊥0C，∠B0A=60°，sin∠B′A0=$\frac{9}{10}$，则点B′到0A的距离为（ ）| A． | $\frac{9\sqrt{3}}{10}$cm | B． | $\frac{18\sqrt{3}}{10}$cm | C． | $\frac{9\sqrt{3}}{5}$cm | D． | $\frac{18\sqrt{3}}{5}$cm |
课外阅读是提高学生素养的重要途径，某校团委为了解学生课外阅读情况，随机抽查了本校n名学生，统计它们平均每天课外阅读时间t（时），并根据时间t的长短分为A、B、C、D四类，（A）0＜t＜0.5，（B）0.5≤t＜1，（C）1≤t＜1.5，（D）t≥1.5，并根据抽查的人数绘制如下统计图．
17．若关于x的方程x2+2x+a=0有两个实数根，则a的取值范围是（ ）
| A． | a＜1 | B． | a＞1 | C． | a≤1 | D． | a≥1 |
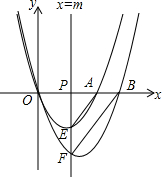如图，动直线x=m（m＞0）分别交x轴，抛物线y=x2-3x和y=x2-4x于点P，E，F，设点A，B为抛物线y=x2-3x，y=x2-4x与x轴的一个交点，连结AE，BF．
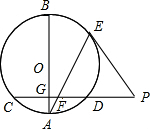如图，AB是圆O的一条直径，弦CD垂直于AB，垂足为点G、E是劣弧BD上一点，点E处的切线与CD的延长线交于点P，连接AE，交CD于点F．