题目内容
10.(1)解不等式组:$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x}\\{1-3(x-1)<8-x}\end{array}\right.$(2)解方程:5(x-3)2=2(3-x)
分析 (1)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
(2)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x①}\\{1-3(x-1)<8-x②}\end{array}\right.$
∵解不等式①得:x≤3,
解不等式②得:x>-2,
∴不等式组的解集为-2<x≤3;
(2)5(x-3)2=2(3-x),
5(x-3)2+2(3-x)=0,
(x-3)[5(x-3)+2]=0,
x-3=0,5(x-3)+2=0,
x1=3,x2=$\frac{13}{5}$.
点评 本题考查了解一元一次不等式组,解二元一次方程组的应用,能根据不等式的解集找出不等式组的解集是解(1)的关键,能把二元一次方程组转化成一元一次方程是解(2)的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.-5的绝对值是( )
| A. | 5 | B. | -$\frac{1}{5}$ | C. | -5 | D. | $\frac{1}{5}$ |
19.中央电视台2016年春晚支付宝互动集五福分大奖活动赢得几亿观众的参与,最终全国约79万观众平均分了2.15亿元大奖,把数2.15亿用科学记数法表示为( )
| A. | 2.15×107 | B. | 0.125×108 | C. | 2.15×108 | D. | 0.125×109 |
20.已知圆的半径是2$\sqrt{3}$,则该圆的内接正三角形的面积是( )
| A. | 9 | B. | 9$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
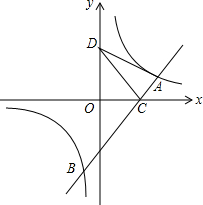 如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC.
如图所示,已知A(4,m),B(-1,n)在反比例函数y=$\frac{8}{x}$的图象上,直线AB与x轴交于C,如果点D在y轴上,且DA=DC. 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.