题目内容
12.阅读材料并解决问题:$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=$\sqrt{3}$-$\sqrt{2}$,像上述解题过程中,$\sqrt{3}$+$\sqrt{2}$与$\sqrt{3}$-$\sqrt{2}$相乘的积不含二次根式,我们可以将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化.(1)$\sqrt{2}$的有理化因式是$\sqrt{2}$;$\sqrt{5}$-2的有理化因式是$\sqrt{5}$+2;
(2)将下列式子进行分母有理化:①$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$;②$\frac{3}{3+\sqrt{6}}$=3-$\sqrt{6}$;
(3)已知a=$\frac{2}{2+\sqrt{3}}$,b=4-2$\sqrt{3}$,利用上述知识比较a与b的大小.
分析 (1)直接利用有理化因式的概念分析得出答案;
(2)利用有理化因式的概念化简求出答案;
(3)直接利用有理化因式的概念化简求出答案.
解答 解:(1)$\sqrt{2}$的有理化因式是:$\sqrt{2}$,
$\sqrt{5}$-2的有理化因式是:$\sqrt{5}$+2;
故答案为:$\sqrt{2}$,$\sqrt{5}$+2;
(2)①$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$;
②$\frac{3}{3+\sqrt{6}}$=3-$\sqrt{6}$;
故答案为:$\frac{2\sqrt{5}}{5}$;3-$\sqrt{6}$;
(3)∵a=$\frac{2}{2+\sqrt{3}}$=$\frac{2(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}$=4-2$\sqrt{3}$,
∴a=b.
点评 此题主要考查了有理化因式的概念,正确化简二次根式是解题关键.

练习册系列答案
相关题目
4.下列方程①x2-2x-1=0;②ax2+bx+c=0;③$\frac{1}{{x}^{2}}$+3x-5=0;④-x2=0;⑤(x-1)2+y2=2;⑥(x-1)(x-3)=x2,其中一元二次方程共有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.有理数a等于它的倒数,有理数b等于它的相反数,则a2003+b2003的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
2.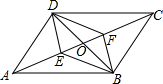 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )| A. | ∠ADE=∠CBF | B. | ∠ABE=∠CDF | C. | DE=BF | D. | OE=OF |
 在Rt△EDF中,ED+DF=10,ED=EG,FD=FH.求△HDG外接圆的半径的最大值.
在Rt△EDF中,ED+DF=10,ED=EG,FD=FH.求△HDG外接圆的半径的最大值.
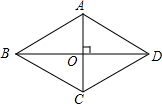 如图,四边形ABCD的对角线互相垂直,且满足AO=CO,请你添加一个适当的条件AC、BD互相平分(答案不唯一),使四边形ABCD成为菱形(只需添加一个即可)
如图,四边形ABCD的对角线互相垂直,且满足AO=CO,请你添加一个适当的条件AC、BD互相平分(答案不唯一),使四边形ABCD成为菱形(只需添加一个即可) 如图,已知AE∥BD,∠1=130°,∠2=30°,求∠C的度数.
如图,已知AE∥BD,∠1=130°,∠2=30°,求∠C的度数.