Question

3．在Rt△EDF中，ED+DF=10，ED=EG，FD=FH．求△HDG外接圆的半径的最大值．

Answer 1

分析 设△HDG外接圆的圆心为O，连接OH，OG，根据已知条件得到∠HOG=90°，设DE=x，OG=OH=R，则FD=10-x，根据勾股定理得到GH=$\sqrt{2}$R，于是求得EF=EG+FH-GH=ED+FD-GH=10-$\sqrt{2}$R，根据勾股定理列方程R²-10$\sqrt{2}$R=x²-10x，求得R=5$\sqrt{2}$-$\sqrt{{x}^{2}-10x+50}$=5$\sqrt{2}$-$\sqrt{（x-5）^{2}+25}$，于是得到结论．

解答 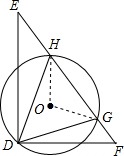解：设△HDG外接圆的圆心为O，连接OH，OG，
∵ED=EG，FD=FH，
∴∠EGD=$\frac{180°-∠E}{2}$，∠FHD=$\frac{180°-∠F}{2}$，
∴∠GDH=180°-∠EGD-∠FHD=$\frac{∠E+∠F}{2}$=45°，
∴∠HOG=90°，
设DE=x，OG=OH=R，则FD=10-x，GH=$\sqrt{2}$R，
∴EF=EG+FH-GH=ED+FD-GH=10-$\sqrt{2}$R，
∵EF²+ED²+FD²，
∴（10-$\sqrt{2}$R）²=x²+（10-x）²，
∴R²-10$\sqrt{2}$R=x²-10x，
∴R=5$\sqrt{2}$-$\sqrt{{x}^{2}-10x+50}$=5$\sqrt{2}$-$\sqrt{（x-5）^{2}+25}$，
∴R_最大=5$\sqrt{2}$-5，此时x=5，即ED=FD=5．

点评 本题考查了三角形的外接圆与外心，等腰三角形的性质，三角形的内角和，勾股定理，连接OH，OG构造直角三角形是解题的关键．