题目内容
2.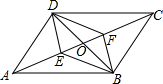 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )| A. | ∠ADE=∠CBF | B. | ∠ABE=∠CDF | C. | DE=BF | D. | OE=OF |
分析 根据平行四边形的性质,以及平行四边形的判定定理即可作出判断.
解答 解:A、 在平行四边形ABCD中,
在平行四边形ABCD中,
∵AO=CO,DO=BO,AD∥BC,AD=BC,
∴∠DAE=∠BCF,
若∠ADE=∠CBF,
在△ADE与△BCF中,
$\left\{\begin{array}{l}{∠DAE=∠BCF}\\{AD=BC}\\{∠ADE=∠CBF}\end{array}\right.$,
∴△ADE≌△BCF,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
B、若∠ABE=∠CDF,
在△ABE与△CDF中,
$\left\{\begin{array}{l}{∠BAE=∠DCF}\\{AB=CD}\\{∠ABE=∠CDF}\end{array}\right.$,
∴△ABE≌△CDF,
∴AE=CF,
∵AO=CO,
∴OE=OF,
∵OD=OB,
∴四边形DEBF是平行四边形;
C、若DE与AC不垂直,则满足AC上一定有一点DM=DE,同理有一点N使BF=BN,则四边形DEBF不一定是平行四边形,则选项错误;
D、若OE=OF,
∵OD=OB,
∴四边形DEBF是平行四边形;
故选C.
点评 本题考查了平行四边形的性质以及判定定理,熟练掌握定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列说法不正确的是( )
| A. | 0.4的算术平方根是0.2 | B. | -9是81的一个平方根 | ||
| C. | -27的立方根是-3 | D. | 1-$\sqrt{2}$的相反数是$\sqrt{2}$-1 |
14.在x=1,y=5x,x2=0,xy=2这四个方程中,是一元一次方程的是( )
| A. | x=1 | B. | y=5x | C. | x2=0 | D. | xy=2 |
11.某种病毒的直径是0.000018毫米,0.000018这个数用科学记数法表示为( )
| A. | 18×10-6 | B. | 1.8×10-6 | C. | 0.18×10-4 | D. | 1.8×10-5 |
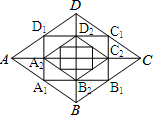 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.
如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.