题目内容
在△ABC中，点D从A出发，在AB边上以每秒一个单位的速度向B运动，同时点F从B出发，在BC边上以相同的速度向C运动，过点D作DE∥BC交AC于点E．运动时间为t秒．
（1）若AB=5，BC=6，当t为何值时，四边形DFCE为平行四边形；
（2）连接AF、CD．若BD=DE，求证：∠BAF=∠BCD；
（3）AF交DE于点M，在DC上取点N，使MN∥AC，连接FN．
①求证：
=
；
②若AB=5，BC=6，AC=4，当MN=FN时，请直接写出t的值．
（1）若AB=5，BC=6，当t为何值时，四边形DFCE为平行四边形；
（2）连接AF、CD．若BD=DE，求证：∠BAF=∠BCD；
（3）AF交DE于点M，在DC上取点N，使MN∥AC，连接FN．
①求证：
| BF |
| CF |
| DN |
| CN |
②若AB=5，BC=6，AC=4，当MN=FN时，请直接写出t的值．
考点：相似形综合题
专题：
分析：（1）若四边形DFCE是平行四边形，则有DE∥BC，当DF∥AC，根据平行线分线段成比例定理得到关于t的方程，解答即可求得．
（2）由DE∥BC，可以证得△ADE∽△ABC，继而证明△ABF∽△CBD，得到，∠BAF=∠BCD．
（3）①由DE∥BC得到△ADM∽△ABF，∴
=
，同理得：
=
，∴
=
．∴
=
，∵MN∥EC，∴
=
，∴
=
．
②由①的结论可以得到答案．
（2）由DE∥BC，可以证得△ADE∽△ABC，继而证明△ABF∽△CBD，得到，∠BAF=∠BCD．
（3）①由DE∥BC得到△ADM∽△ABF，∴
| AM |
| AF |
| DM |
| BF |
| AM |
| AF |
| EM |
| CF |
| DM |
| BF |
| EM |
| CF |
| DM |
| ME |
| BF |
| CF |
| DM |
| ME |
| DN |
| CN |
| BF |
| CF |
| DN |
| CN |
②由①的结论可以得到答案．
解答：解：（1）∵DE∥BC，当DF∥AC时，四边形DFCE是平行四边形．
∴
=
，
∵AD=BF=t，
∴BD=5-t，
∴
=
，
∴t=
．
（2）证明：∵DE∥BC，
∴△ADE∽△ABC，
∴
=
，
∵AD=BF，DE=DB，
∴
=
，
∵∠ABF=∠CBD，
∴△ABF∽△CBD，
∴∠BAF=∠BCD．
（3）①证明：∵DE∥BC，
∴△ADM∽△ABF，
∴
=
，
同理得：
=
，
∴
=
．
∴
=
，
∵MN∥EC，
∴
=
，
∴
=
．
②t=
．
∴
| BD |
| AB |
| BF |
| BC |
∵AD=BF=t，
∴BD=5-t，
∴
| 5-t |
| 5 |
| t |
| 6 |
∴t=
| 30 |
| 11 |
（2）证明：∵DE∥BC，
∴△ADE∽△ABC，
∴
| AD |
| AB |
| DE |
| BC |
∵AD=BF，DE=DB，
∴
| BF |
| AB |
| DB |
| BC |
∵∠ABF=∠CBD，
∴△ABF∽△CBD，
∴∠BAF=∠BCD．
（3）①证明：∵DE∥BC，
∴△ADM∽△ABF，
∴
| AM |
| AF |
| DM |
| BF |
同理得：
| AM |
| AF |
| EM |
| CF |
∴
| DM |
| BF |
| EM |
| CF |
∴
| DM |
| ME |
| BF |
| CF |
∵MN∥EC，
∴
| DM |
| ME |
| DN |
| CN |
∴
| BF |
| CF |
| DN |
| CN |
②t=
| 10 |
| 3 |
点评：本题主要考查了平行线分线段成比例定理以及三角形相似的判定与性质的综合应用，解答本题的关键是如何根据两直线平行确定对应的三角形相似．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
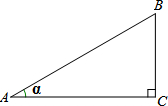如图，定义：在Rt△ABC中，∠C=90°，锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα=
如果，O是直线AB上的一点，射线OC、OE分别平分∠AOD和∠BOD．
