题目内容
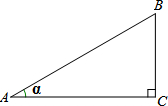如图，定义：在Rt△ABC中，∠C=90°，锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα=| 角α的邻边 |
| 角α的对边 |
| AC |
| BC |
（1）ctan60°=
（2）求ctan15°的值．
考点：解直角三角形
专题：新定义
分析：（1）在Rt△ABC中，设∠B=60°，则∠A=30°，根据直角三角形的性质用BC表示出AC的值，再根据余切的定义进行解答即可；
（2）作△DEG，使DE=GE，∠D=15°．过点G作GH⊥DE的延长线于点H．先根据等边对等角的性质及三角形外角的性质得出∠2=∠1+∠D=30°，再设GH=x，解Rt△GEH，得出EH=
x，GE=DE=2x，则DH=DE+EH=2x+
x，然后在Rt△GDH中根据余切的定义进行解答即可．
（2）作△DEG，使DE=GE，∠D=15°．过点G作GH⊥DE的延长线于点H．先根据等边对等角的性质及三角形外角的性质得出∠2=∠1+∠D=30°，再设GH=x，解Rt△GEH，得出EH=
| 3 |
| 3 |
解答：解：（1）如图，在Rt△ABC中，设∠B=60°，
∴∠A=90°-60°=30°，
∴AC=
BC，
∴ctan60°=ctan∠B=
=
=
．
故答案为
；
（2）如图，作△DEG，使DE=GE，∠D=15°．
过点G作GH⊥DE的延长线于点H．
∵DE=GE，∠D=15°，
∴∠1=∠D=15°，
∴∠2=∠1+∠D=30°．
在Rt△GEH中，∵∠H=90°，∠2=30°，设GH=x，
∴EH=
x，GE=DE=2x，
∴DH=DE+EH=2x+
x，
∴ctan15°=
=
=2+
．
解：（1）如图，在Rt△ABC中，设∠B=60°，∴∠A=90°-60°=30°，
∴AC=
| 3 |
∴ctan60°=ctan∠B=
| BC |
| AC |
| BC | ||
|
| ||
| 3 |
故答案为
| ||
| 3 |
（2）如图，作△DEG，使DE=GE，∠D=15°．过点G作GH⊥DE的延长线于点H．
∵DE=GE，∠D=15°，
∴∠1=∠D=15°，
∴∠2=∠1+∠D=30°．
在Rt△GEH中，∵∠H=90°，∠2=30°，设GH=x，
∴EH=
| 3 |
∴DH=DE+EH=2x+
| 3 |
∴ctan15°=
| DH |
| GH |
2x+
| ||
| x |
| 3 |
点评：本题考查的是解直角三角形，锐角三角函数的定义，直角三角形、等腰三角形的性质及三角形外角的性质，熟知锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
北京故宫的占地面积约为7.20×105米2，下列说法正确的是（ ）
| A、有两个有效数字，精确到十分位 |
| B、有两个有效数字，精确到万位 |
| C、有三个有效数字，精确到百分位 |
| D、有三个有效数字，精确到千位 |
某学校的围墙CD到教学楼AB的距离CE=22.5米，CD=3米．该学校为了纪念建校61周年准备彩旗连接线AC，∠ACE=22°．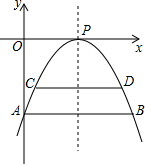
有一座抛物线形状的拱桥，当水位涨到AB时，水面AB的宽度为14米，如果水位再上升4米，就到达警戒水位CD，这时水面的宽度是10米．
