题目内容
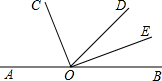 如果,O是直线AB上的一点,射线OC、OE分别平分∠AOD和∠BOD.
如果,O是直线AB上的一点,射线OC、OE分别平分∠AOD和∠BOD.(1)与∠COD互余的角有
(2)与∠AOC互余的角有
(3)已知∠AOC=58°,求∠BOE的度数.
考点:余角和补角,角平分线的定义
专题:
分析:(1)根据角平分线的性质可得∠DOE=∠EOB=
∠AOD,∠DOC=∠AOC=
∠DOB,然后求出∠DOE+∠DOC=90°,进而得到∠COD+∠BOE=90°,然后可得答案;
(2)根据等角的余角相等可得与∠COD互余的角有∠BOE,∠DOE;
(3)根据余角的定义计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据等角的余角相等可得与∠COD互余的角有∠BOE,∠DOE;
(3)根据余角的定义计算即可.
解答:解:(1)OE、OC分别是∠AOD和∠BOD的平分线,
∴∠DOE=∠EOB=
∠AOD,∠DOC=∠AOC=
∠DOB,
∵∠AOB=∠AOD+∠BOD=180°,
∴
(∠AOD+∠BOD)=90°,
即∠DOE+∠DOC=90°,
∴∠COD+∠BOE=90°,
∴与∠COD互余的角有∠BOE,∠DOE.
故答案为:∠BOE,∠DOE;
(2)∵∠DOC=∠AOC,
∴与∠COD互余的角有∠BOE,∠DOE,
故答案为:∠BOE,∠DOE.
(3)∵∠AOC=58°,
∴∠BOE=90°-58°=32°.
∴∠DOE=∠EOB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=∠AOD+∠BOD=180°,
∴
| 1 |
| 2 |
即∠DOE+∠DOC=90°,
∴∠COD+∠BOE=90°,
∴与∠COD互余的角有∠BOE,∠DOE.
故答案为:∠BOE,∠DOE;
(2)∵∠DOC=∠AOC,
∴与∠COD互余的角有∠BOE,∠DOE,
故答案为:∠BOE,∠DOE.
(3)∵∠AOC=58°,
∴∠BOE=90°-58°=32°.
点评:此题主要考查了余角的性质,以及余角的概念,关键是掌握互为余角的两个角的和为90度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
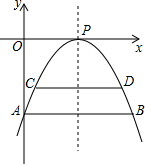 有一座抛物线形状的拱桥,当水位涨到AB时,水面AB的宽度为14米,如果水位再上升4米,就到达警戒水位CD,这时水面的宽度是10米.
有一座抛物线形状的拱桥,当水位涨到AB时,水面AB的宽度为14米,如果水位再上升4米,就到达警戒水位CD,这时水面的宽度是10米.
 (1)已知线段AB在平面内,在平面内找一点P使∠APB=90°.
(1)已知线段AB在平面内,在平面内找一点P使∠APB=90°.
 如图,AB、CD、EF相交于点O,∠1=20°,∠BOC=80°,则∠2=
如图,AB、CD、EF相交于点O,∠1=20°,∠BOC=80°,则∠2=