��Ŀ����
��ͼ����֪������y=ax2+bx-2��x�������������A��4��0����B��1��0������y��Ľ�����C��
��1����������ߵĽ���ʽ��
��2����ֱ��AC�Ϸ��ĸ����������Ƿ����һ��D��ʹ�á�DCA�������������ڣ������D�����꼰��DCA��������ֵ���������ڣ���˵�����ɣ�
��3���������ߵĶ�����F���Գ�����AC�Ľ�����N��P����AC�Ϸ��ĸ���������һ���㣬��P��PM��x�ᣬ��AC��M����P��ĺ�������m���ʣ�
��mȡ��ֵʱ������P��M��N��F��ƽ��ͼ�β������Σ�
���ı���PMNF�Ƿ��п����ǵ������Σ����п��ܣ��������ʱm��ֵ���������ܣ���˵�����ɣ�
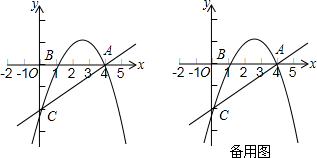
��1����������ߵĽ���ʽ��
��2����ֱ��AC�Ϸ��ĸ����������Ƿ����һ��D��ʹ�á�DCA�������������ڣ������D�����꼰��DCA��������ֵ���������ڣ���˵�����ɣ�
��3���������ߵĶ�����F���Գ�����AC�Ľ�����N��P����AC�Ϸ��ĸ���������һ���㣬��P��PM��x�ᣬ��AC��M����P��ĺ�������m���ʣ�
��mȡ��ֵʱ������P��M��N��F��ƽ��ͼ�β������Σ�
���ı���PMNF�Ƿ��п����ǵ������Σ����п��ܣ��������ʱm��ֵ���������ܣ���˵�����ɣ�

���㣺���κ����ۺ���
ר�⣺
��������1���������߾���A��4��0����B��1��0����C��0��-2�����㣬���ô���ϵ����������ø������ߵĽ���ʽ��
��2����D��ĺ�����Ϊt��0��t��4������D���������Ϊ-
t2+
t-2����D��y���ƽ���߽�AC��E���������DE�ij����̶������S��DCA=-��t-2��2+4��Ȼ���ɶ��κ��������ʣ�������õ�D�����꼰��DCA��������ֵ��
��3��������P��m��-
m2+
m-2��������PM��x�ᣬFN�ǶԳ��ᣬ�ɵ�PM��FN����PM=FNʱP��M��N��F��ƽ��ͼ��ƽ���ı��Σ��������Σ��Ӷ����m��ֵΪ
�����������֪���P��Ĺ��ڶ��κ����ĶԳ���ĶԳƵ�P�䣬������A���غϣ�����ֻ�ܹ��ɵ��������Σ������ɵ������Σ�
��2����D��ĺ�����Ϊt��0��t��4������D���������Ϊ-
| 1 |
| 2 |
| 5 |
| 2 |
��3��������P��m��-
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
����⣺��1���߸������߹���C��0��-2����
�����������ߵĽ���ʽΪy=ax2+bx-2��
��A��4��0����B��1��0������y=ax2+bx-2��
��
��
��ã�
��
��������ߵĽ���ʽΪy=-
x2+
x-2��
��2�����ڣ�
��ͼ1����D��ĺ�����Ϊt��0��t��4������D���������Ϊ-
t2+
t-2��
��D��y���ƽ���߽�AC��E��
��ֱ��AC�Ľ���ʽΪ��y=mx+n��
��
��ã�
��
����������ֱ��AC�Ľ���ʽΪy=
x-2��
��E���������t��
t-2����
��DE=-
t2+
t-2-��
t-2��=-
t2+2t��
��S��DCA=S��CDE+S��ADE=
��DE��OA=
����-
t2+2t����4=-t2+4t=-��t-2��2+4��
�൱t=2ʱ��S���=4��
�൱D��2��1������DAC��������ֵΪ4��
��3�����ڣ���y=-
x2+
x-2=-
��x-
��2+
��
��F��
��
��
�٢�P��F�غ�ʱ��P��M��N��F��һ��ֱ�ߣ����ܹ������Σ���ʱm=
��
����ͼ2����P��m��-
m2+
m-2����0��m��
������PM��x�ᣬFN�ǶԳ��ᣬ
��PM��FN
�൱PM=FNʱP��M��N��F��ƽ��ͼ��ƽ���ı��Σ��������Σ�
����N��
��-
����M��m��
m-2��
��PM��-
m2+
m-2��-��
m-2��=-
m2+2m��
FN=
-��-
��=
��PM=FNʱ
����-
m2+2m=
�����m=
��m=
����ȥ��
�൱m=
��m=
ʱ��P��M��N��F��ƽ��ͼ�β������Σ�

��3���ı���PMNF�����ǵ������Σ�
���������ϵĵ�P�䴹ֱ��x���ֱ�߽�AC��M�䣬
����m=
ʱ���ı���PMNF��ƽ���ı��Σ�����PF=MN��
���������ߵĶԳ��ԣ���m=
ʱ����P��F=M��N����ʱ����P��FNM���ǵ������Σ�
�����������ߵĽ���ʽΪy=ax2+bx-2��
��A��4��0����B��1��0������y=ax2+bx-2��
��
|
��ã�
|
��������ߵĽ���ʽΪy=-
| 1 |
| 2 |
| 5 |
| 2 |
��2�����ڣ�
��ͼ1����D��ĺ�����Ϊt��0��t��4������D���������Ϊ-
| 1 |
| 2 |
| 5 |
| 2 |
��D��y���ƽ���߽�AC��E��
��ֱ��AC�Ľ���ʽΪ��y=mx+n��
��
|
��ã�
|
����������ֱ��AC�Ľ���ʽΪy=
| 1 |
| 2 |
��E���������t��
| 1 |
| 2 |
��DE=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��S��DCA=S��CDE+S��ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�൱t=2ʱ��S���=4��
�൱D��2��1������DAC��������ֵΪ4��
��3�����ڣ���y=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 8 |
��F��
| 5 |
| 2 |
| 9 |
| 8 |
�٢�P��F�غ�ʱ��P��M��N��F��һ��ֱ�ߣ����ܹ������Σ���ʱm=
| 5 |
| 2 |
����ͼ2����P��m��-
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
��PM��FN
�൱PM=FNʱP��M��N��F��ƽ��ͼ��ƽ���ı��Σ��������Σ�
����N��
| 5 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
��PM��-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
FN=
| 9 |
| 8 |
| 3 |
| 4 |
| 15 |
| 8 |
��PM=FNʱ
����-
| 1 |
| 2 |
| 15 |
| 8 |
| 3 |
| 2 |
| 5 |
| 2 |
�൱m=
| 3 |
| 2 |
| 5 |
| 2 |

��3���ı���PMNF�����ǵ������Σ�
���������ϵĵ�P�䴹ֱ��x���ֱ�߽�AC��M�䣬
����m=
| 3 |
| 2 |
���������ߵĶԳ��ԣ���m=
| 7 |
| 2 |
���������⿼���˴���ϵ���������Ľ���ʽ�����������ε��ж��������Լ����κ�������ֵ���⣮�����ѶȽϴ�ע�����շ���˼�롢��������˼�������ν��˼���Ӧ��

��ϰ��ϵ�д�
�����Ŀ

 ��1����֪�߶�AB��ƽ���ڣ���ƽ������һ��Pʹ��APB=90�㣮
��1����֪�߶�AB��ƽ���ڣ���ƽ������һ��Pʹ��APB=90�㣮 �ڷ���ֽ�У���ͼ����A��B��C��Ϊ�����㣨С�����εĶ���и�㣩����C��ֱ��AB�⣬������������⣺
�ڷ���ֽ�У���ͼ����A��B��C��Ϊ�����㣨С�����εĶ���и�㣩����C��ֱ��AB�⣬������������⣺